
題目列表(包括答案和解析)
7.設(shè) ,且
,且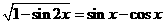 ,則 ( )
,則 ( )
A.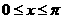 B.
B.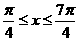 C.
C.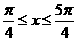 D.
D.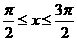
解:∵由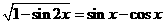 得|sinx-cosx|=sinx-cosx,又
得|sinx-cosx|=sinx-cosx,又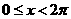 ,
,
∴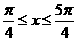 ,選C
,選C
6.若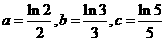 ,則 ( )
,則 ( )
A.a<b<c B.c<b<a C.c<a<b D.b<a<c
解:由題意得a=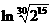 ,b=
,b=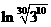 ,c=
,c=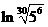 ,
,
∵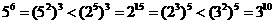 ,∴c<a<b,選C
,∴c<a<b,選C
5.設(shè)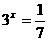 ,則 ( )
,則 ( )
A.-2<x<-1 B.-3<x<-2 C.-1<x<0 D.0<x<1
解: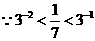 ,
,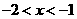 ,選A
,選A
4.設(shè)三棱柱ABC-A1B1C1的體積為V,P、Q分別是側(cè)棱AA1、CC1上的點(diǎn),且PA=QC1,則四棱錐B-APQC的體積為 ( )
A.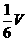 B.
B.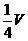 C.
C.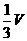 D.
D.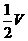
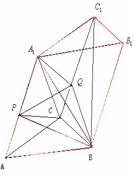 解:如圖,
解:如圖,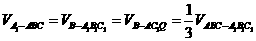
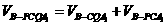 ,∵AF=QC1,
,∵AF=QC1,
∴APQC1,APQC都是平行四邊形,
∴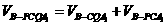 =
=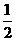 (
(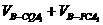 )
)
=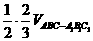 =
=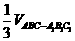 ,選C
,選C
3.在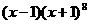 的展開式中
的展開式中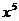 的系數(shù)是 ( )
的系數(shù)是 ( )
A.-14 B.14 C.-28 D.28
解:(x+1)8展開式中x4,x5的系數(shù)分別為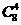 ,
,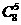 ,∴(x-1)(x+1)8展開式中x5的系數(shù)為
,∴(x-1)(x+1)8展開式中x5的系數(shù)為
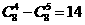 ,選B
,選B
2.已知過點(diǎn)A(-2,m)和B(m,4)的直線與直線2x+y-1=0平行,則m的值為 ( )
A.0 B.-8 C.2 D.10
解:直線2x+y-1=0的一個(gè)方向向量為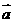 =(1,-2),
=(1,-2),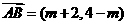 ,由
,由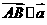
即(m+2)×(-2)-1×(4-m)=0,m=-8,選B
1.已知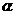 為第三象限角,則
為第三象限角,則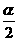 所在的象限是 ( )
所在的象限是 ( )
A.第一或第二象限 B.第二或第三象限
C.第一或第三象限 D.第二或第四象限
解:α第三象限,即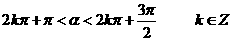 ,
,
∴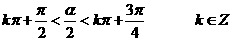 ,可知
,可知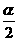 在第二象限或第四象限,選D
在第二象限或第四象限,選D
(17)(本大題滿分12分)
設(shè)函數(shù)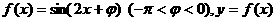 圖像的一條對稱軸是直線
圖像的一條對稱軸是直線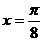 。
。
(Ⅰ)求 ;
;
(Ⅱ)求函數(shù) 的單調(diào)增區(qū)間;
的單調(diào)增區(qū)間;
(Ⅲ)畫出函數(shù) 在區(qū)間
在區(qū)間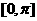 上的圖像。
上的圖像。
(18)(本大題滿分12分)
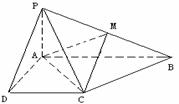
已知四棱錐P-ABCD的底面為直角梯形,AB∥DC,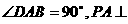 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=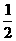 AB=1,M是PB的中點(diǎn)。
AB=1,M是PB的中點(diǎn)。
(Ⅰ)證明:面PAD⊥面PCD;
(Ⅱ)求AC與PB所成的角;
(Ⅲ)求面AMC與面BMC所成二面角的大小。
(19)(本大題滿分12分)
已知二次函數(shù)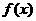 的二次項(xiàng)系數(shù)為
的二次項(xiàng)系數(shù)為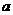 ,且不等式
,且不等式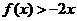 的解集為
的解集為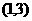 。
。
(Ⅰ)若方程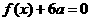 有兩個(gè)相等的根,求
有兩個(gè)相等的根,求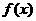 的解析式;
的解析式;
(Ⅱ)若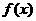 的最大值為正數(shù),求
的最大值為正數(shù),求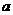 的取值范圍。
的取值范圍。
(20)(本大題滿分12分)
9粒種子分種在甲、乙、丙3個(gè)坑內(nèi),每坑3粒,每粒種子發(fā)芽的概率為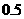 ,若一個(gè)坑內(nèi)至少有1粒種子發(fā)芽,則這個(gè)坑不需要補(bǔ)種;若一個(gè)坑內(nèi)的種子都沒發(fā)芽,則這個(gè)坑需要補(bǔ)種。
,若一個(gè)坑內(nèi)至少有1粒種子發(fā)芽,則這個(gè)坑不需要補(bǔ)種;若一個(gè)坑內(nèi)的種子都沒發(fā)芽,則這個(gè)坑需要補(bǔ)種。
(Ⅰ)求甲坑不需要補(bǔ)種的概率;
(Ⅱ)求3個(gè)坑中恰有1個(gè)坑不需要補(bǔ)種的概率;
(Ⅲ)求有坑需要補(bǔ)種的概率。
(精確到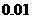 )
)
(21)(本大題滿分12分)
設(shè)正項(xiàng)等比數(shù)列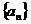 的首項(xiàng)
的首項(xiàng)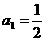 ,前n項(xiàng)和為
,前n項(xiàng)和為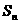 ,且
,且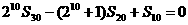 。
。
(Ⅰ)求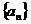 的通項(xiàng);
的通項(xiàng);
(Ⅱ)求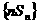 的前n項(xiàng)和
的前n項(xiàng)和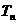 。
。
(22)(本大題滿分14分)
已知橢圓的中心為坐標(biāo)原點(diǎn)O,焦點(diǎn)在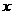 軸上,斜率為1且過橢圓右焦點(diǎn)F的直線交橢圓于A、B兩點(diǎn),
軸上,斜率為1且過橢圓右焦點(diǎn)F的直線交橢圓于A、B兩點(diǎn),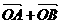 與
與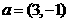 共線。
共線。
(Ⅰ)求橢圓的離心率;
(Ⅱ)設(shè)M為橢圓上任意一點(diǎn),且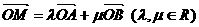 ,證明
,證明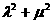 為定值。
為定值。






(13)若正整數(shù)m滿足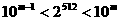 ,則m = 。
,則m = 。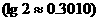
解:∵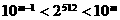 ,∴
,∴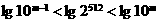 ,即
,即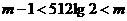 ,
,
∴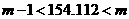 ,即
,即 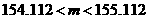 ,∴
,∴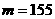 .
.
(14)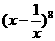 的展開式中,常數(shù)項(xiàng)為
。(用數(shù)字作答
的展開式中,常數(shù)項(xiàng)為
。(用數(shù)字作答
解: 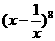 的通項(xiàng)公式為
的通項(xiàng)公式為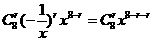 ,令8-2r=0,得r=4,∴常數(shù)項(xiàng)為70.
,令8-2r=0,得r=4,∴常數(shù)項(xiàng)為70.
(15)從6名男生和4名女生中,選出3名代表,要求至少包含1名女生,則不同的選法共有 種。
解:用剔除法.: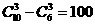 ,∴從6名男生和4名女生中,選出3名代表,要求至少包含1名女生,則不同的選法共有100種。
,∴從6名男生和4名女生中,選出3名代表,要求至少包含1名女生,則不同的選法共有100種。
(16)在正方形 中,過對角線
中,過對角線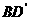 的一個(gè)平面交
的一個(gè)平面交 于E,交
于E,交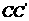 于F,
于F,
①
四邊形 一定是平行四邊形
一定是平行四邊形
②
四邊形 有可能是正方形
有可能是正方形
③
四邊形 在底面ABCD內(nèi)的投影一定是正方形
在底面ABCD內(nèi)的投影一定是正方形
④
四邊形 有可能垂直于平面
有可能垂直于平面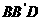
以上結(jié)論正確的為 。(寫出所有正確結(jié)論的編號)
 解:①平面
解:①平面 與相對側(cè)面相交,交線互相平行,
與相對側(cè)面相交,交線互相平行,
∴四邊形 一定是平行四邊形;
一定是平行四邊形;
②四邊形 若是正方形,則
若是正方形,則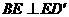 ,又
,又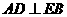 ,
,
∴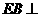 平面
平面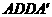 ,產(chǎn)生矛盾;
,產(chǎn)生矛盾;
③四邊形 在底面ABCD內(nèi)的投影是正方形
在底面ABCD內(nèi)的投影是正方形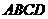 ;
;
④當(dāng)E、F分別是 、
、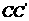 的中點(diǎn)時(shí),
的中點(diǎn)時(shí),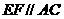 ,又
,又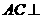 平面
平面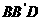 ,
,
∴四邊形 有可能垂直于平面,∴填①③④.
有可能垂直于平面,∴填①③④.
(1)設(shè)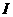 為全集,
為全集,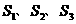 是
是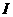 的三個(gè)非空子集,且
的三個(gè)非空子集,且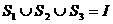 ,則下面論斷正確的是
,則下面論斷正確的是
(A)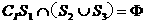 (B)
(B)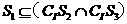
 (C)
(C)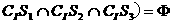 (D)
(D)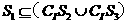
解:∵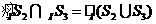 所表示的部分是圖中藍(lán)色
所表示的部分是圖中藍(lán)色
的部分,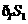 所表示的部分是圖中除去
所表示的部分是圖中除去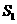 的部分,
的部分,
∴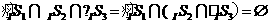 ,故選C.
,故選C.
(2)一個(gè)與球心距離為1的平面截球所得的圓面面積為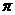 ,則球的表面積為
,則球的表面積為
(A)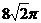 (B)
(B)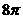 (C)
(C)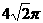 (D)
(D)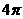
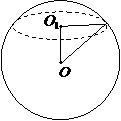 解:∵截面圓面積為
解:∵截面圓面積為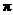 ,∴截面圓半徑
,∴截面圓半徑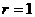 ,
,
∴球的半徑為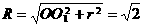 ,
,
∴球的表面積為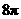 ,故選B.
,故選B.
(3)函數(shù)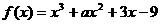 ,已知
,已知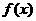 在
在 時(shí)取得極值,則
時(shí)取得極值,則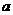 =
=
(A)2 (B)3 (C)4 (D)5
解: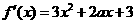 ,令
,令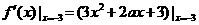 =0,解得a=5,選(D)
=0,解得a=5,選(D)
(4)如圖,在多面體ABCDEF中,已知ABCD是邊長為1的正方形,且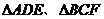 均為正三角形,EF∥AB,EF=2,則該多面體的體積為
均為正三角形,EF∥AB,EF=2,則該多面體的體積為
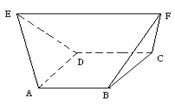 (A)
(A)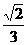 (B)
(B)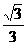
(C)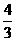 (D)
(D)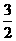
解:如圖,過A、B兩點(diǎn)分別作AM、BN垂直于EF,垂足分別為M、N,連結(jié)DM、CN,可證得DM⊥EF、CN⊥EF,多面體ABCDEF分為三部分,多面體的體積V為
 ,∵
,∵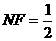 ,
,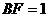 ,∴
,∴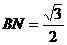 ,
,
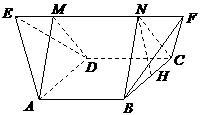 作NH垂直于點(diǎn)H,則H為BC的中點(diǎn),則
作NH垂直于點(diǎn)H,則H為BC的中點(diǎn),則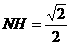 ,∴
,∴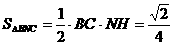 ,∴
,∴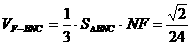 ,
,
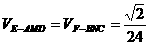 ,
,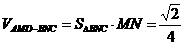 ,∴
,∴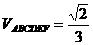 ,故選A.
,故選A.
(5)已知雙曲線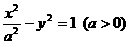 的一條準(zhǔn)線為
的一條準(zhǔn)線為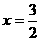 ,則該雙曲線的離心率為
,則該雙曲線的離心率為
(A)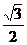 (B)
(B)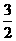 (C)
(C)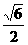 (D)
(D)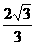
解:由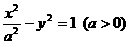 得
得 ,∴
,∴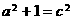 ,拋物線
,拋物線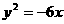 的準(zhǔn)線為
的準(zhǔn)線為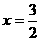 ,因?yàn)殡p曲線
,因?yàn)殡p曲線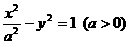 的一條準(zhǔn)線與拋物線
的一條準(zhǔn)線與拋物線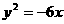 的準(zhǔn)線重合,所以
的準(zhǔn)線重合,所以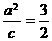 ,解得
,解得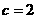 ,所以
,所以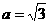 ,所以離心率為
,所以離心率為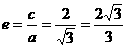 ,故選D.
,故選D.
(6)當(dāng)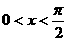 時(shí),函數(shù)
時(shí),函數(shù)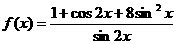 的最小值為
的最小值為
(A)2 (B)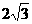 (C)4 (D)
(C)4 (D)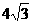
解: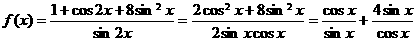
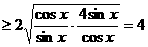 ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng)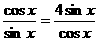 ,即
,即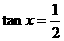 時(shí),取“
時(shí),取“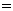 ”,∵
”,∵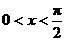 ,∴存在
,∴存在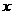 使
使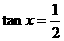 ,這時(shí)
,這時(shí) ,故選(C).
,故選(C).
(7)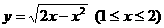 反函數(shù)是
反函數(shù)是
(A)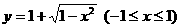
(B)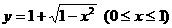
(C)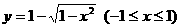
(D)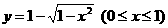
解:由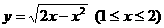 ,得
,得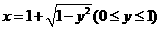 ,故
,故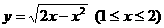 的反函數(shù)為
的反函數(shù)為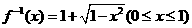 ,選(D)
,選(D)
(8)設(shè) ,函數(shù)
,函數(shù)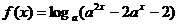 ,則使
,則使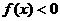 的
的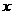 的取值范圍是
的取值范圍是
(A)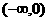 (B)
(B)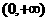 (C)
(C)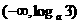 (D)
(D)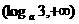
解:∵ ,
,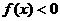 ,∴
,∴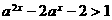 ,解得
,解得 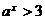 或
或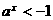 (舍去),
(舍去),
∴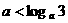 ,故選C.
,故選C.
(9)在坐標(biāo)平面上,不等式組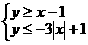 所表示的平面區(qū)域的面積為
所表示的平面區(qū)域的面積為
(A)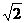 (B)
(B)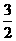 (C)
(C)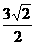 (D)2
(D)2
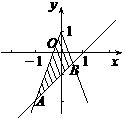 解:原不等式化為
解:原不等式化為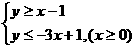 或
或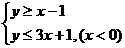 ,
,
所表示的平面區(qū)域如右圖所示,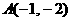 ,
,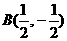 ,
,
∴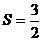 ,故選B
,故選B
(10)在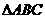 中,已知
中,已知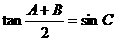 ,給出以下四個(gè)論斷:
,給出以下四個(gè)論斷:
①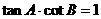 ②
②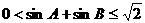
③ ④
④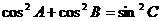
其中正確的是
(A)①③ (B)②④ (C)①④ (D)②③
解:∵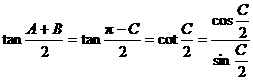 ,
,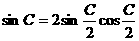 ,
,
∴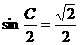 ,∴
,∴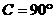 ,
,
∵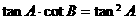 ,∴①不一定成立,
,∴①不一定成立,
∵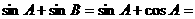
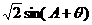 ,∴
,∴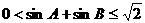 ,∴②成立,
,∴②成立,
∵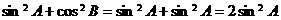 ,∴③不一定成立,
,∴③不一定成立,
∵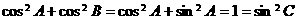 ,∴④成立,故選B.
,∴④成立,故選B.
(11)點(diǎn)O是三角形ABC所在平面內(nèi)的一點(diǎn),滿足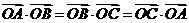 ,則點(diǎn)O是
,則點(diǎn)O是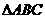 的
的
(A)三個(gè)內(nèi)角的角平分線的交點(diǎn) (B)三條邊的垂直平分線的交點(diǎn) (C)三條中線的交點(diǎn) (D)三條高的交點(diǎn)
解: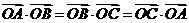 ,即
,即
得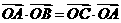 ,
,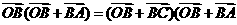
即 ,故
,故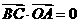 ,
,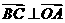 ,同理可證
,同理可證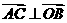 ,∴O是
,∴O是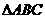 的三條高的交點(diǎn),選(D)
的三條高的交點(diǎn),選(D)
(12)設(shè)直線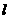 過點(diǎn)
過點(diǎn)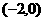 ,且與圓
,且與圓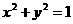 相切,則
相切,則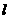 的斜率是
的斜率是
(A)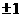 (B)
(B)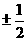 (C)
(C)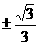 (D)
(D)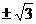
解:設(shè)過點(diǎn)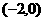 ,且與圓
,且與圓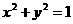 相切的直線
相切的直線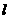 的斜率為k,則直線
的斜率為k,則直線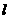 的方程為:y-kx+2k=0,k滿足:1=
的方程為:y-kx+2k=0,k滿足:1=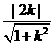 得k=
得k=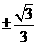 ,選(D).
,選(D).
第Ⅱ卷
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com