
高2009級一診模擬(理科)數學試題
一.選擇題:(每小題5分,共60分)
1.設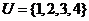 ,且
,且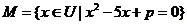 ,若
,若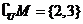 ,則實數
,則實數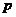 的值為
的值為
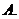
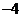
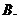
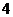
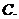
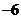
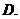
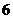
2.等差數列{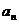 }中,若
}中,若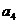 +
+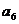 +
+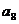 +
+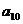 +
+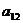 =120,則
=120,則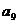 -
-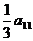 的值是
的值是
A.14 B.
3.已知向量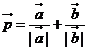 ,其中
,其中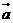 、
、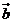 均為非零向量,則
均為非零向量,則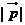 的取值范圍是
的取值范圍是
A.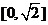 B。
B。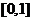 C。
C。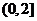 D。
D。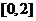
4.編號為1、2、3、4、5的五個人分別去坐編號為1、2、3、4、5的五個座位,其中有且只有兩個的編號與座位號一致的坐法是
A 10種 B 20種 C 30種 D 60種
5.若(1+mx)6=a0+a1x+a2x2+…+a6x6且a1+a2+…+a6=63,則實數m的值為.
A.
1
B.
6.已知數列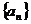 是由正數組成的數列,
是由正數組成的數列,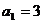 ,且滿足
,且滿足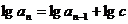 ,其中
,其中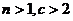 ,則
,則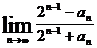 等于
等于
 A. -1
B.
A. -1
B. 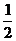 D.
D. 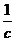
7.一個籃球運動員投籃一次得3分的概率為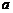 ,得2分的概率為
,得2分的概率為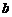 ,不得分的概率為
,不得分的概率為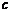 (
(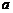 、
、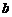 、
、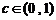 ),已知他投籃一次得分的數學期望為2(不計其它得分情況),則
),已知他投籃一次得分的數學期望為2(不計其它得分情況),則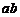 的最大值為
的最大值為
A.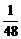 B.
B.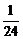 C.
C.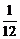 D.
D.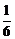
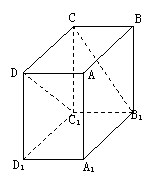
8.在長方體ABCD-A1B
A.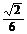 B.
B. 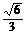 C.
C. 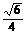 D.
D. 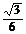
9.設函數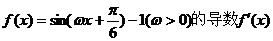 的最大值為3,則f(x)的圖象的一條對稱軸的方程是
的最大值為3,則f(x)的圖象的一條對稱軸的方程是
A.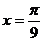 B.
B.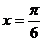 C.
C.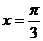 D.
D.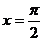
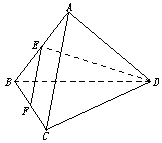 10.如圖在正三棱錐A-BCD中,E、F分別是AB、BC的中點,EF⊥DE,且AC=1,則正三棱錐A-BCD的外接球的體積是
10.如圖在正三棱錐A-BCD中,E、F分別是AB、BC的中點,EF⊥DE,且AC=1,則正三棱錐A-BCD的外接球的體積是

11.已知函數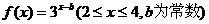 的圖象經過點(2,1),則
的圖象經過點(2,1),則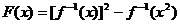 的值域為
的值域為
A.[2,5] B.[1,+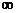 ] C.[2,10] D.[2,13]
] C.[2,10] D.[2,13]
 12.定義在R上的函數
12.定義在R上的函數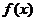 滿足
滿足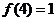 .
.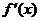 為
為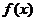 的導函數,已知函數
的導函數,已知函數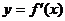 的圖象如右圖所示.若兩正數
的圖象如右圖所示.若兩正數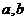 滿足
滿足 ,則
,則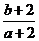 的取值范圍是
的取值范圍是
A.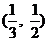 B.
B.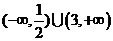 C.
C.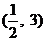 D.
D.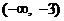
二.填空題:(每小題4分,共16分)
13.已知函數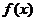 是奇函數,當
是奇函數,當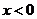 時,
時,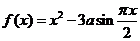 ,且
,且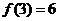 ,則實數
,則實數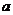 =__________.
=__________.
14.設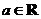 ,函數
,函數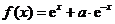 的導函數是
的導函數是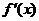 ,且
,且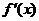 是奇函數 . 若曲線
是奇函數 . 若曲線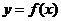 的一條切線的斜率是
的一條切線的斜率是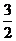 ,則切點的橫坐標為______.
,則切點的橫坐標為______.
15.設函數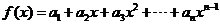 ,
,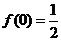 ,數列
,數列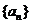 滿足
滿足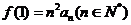 ,則數列
,則數列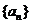 的通項
的通項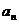 等于
.
等于
.
16.下列命題:
① 函數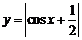 的最小正周期是
的最小正周期是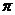 ;
;
②函數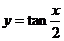 的圖像的對稱中心是
的圖像的對稱中心是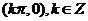 ;
;
③ 函數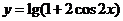 的遞減區間是[
的遞減區間是[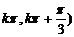
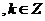 ;
;
④ 函數 的圖像可由函數
的圖像可由函數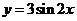 的圖像按向量
的圖像按向量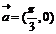 平移得到。其中正確的命題序號是 。
平移得到。其中正確的命題序號是 。
13
14
15
16
三.解答題:
17.(12分)已知△ABC的面積S滿足3≤S≤3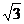 且
且 的夾角為
的夾角為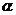 ,
,
(Ⅰ)求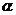 的取值范圍;
的取值范圍;
(Ⅱ)求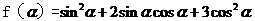 的最小值。
的最小值。
18. (12分)奧運會乒乓球比賽將產生男子單打、女子單打、男子團體、女子團體共四枚金牌,保守估計中國乒乓球男隊獲得每枚金牌的概率均為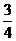 ,中國乒乓球女隊獲得一枚金牌的概率均為
,中國乒乓球女隊獲得一枚金牌的概率均為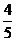 。
。
(I)求按此估計中國乒乓球女隊比中國乒乓球男隊多獲得一枚金牌的概率;
(II)記中國乒乓球隊獲得金牌的數為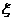 ,按此估計
,按此估計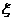 的分布列和數學期望
的分布列和數學期望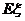 。
。
 19. (12分)已知斜三棱柱
19. (12分)已知斜三棱柱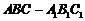 ,
,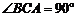 ,
,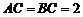 ,
,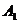 在底面
在底面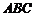 上的射影恰為
上的射影恰為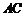 的中點
的中點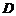 ,又知
,又知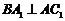 .
.
(Ⅰ)求證: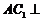 平面
平面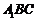 ;
;
(Ⅱ)求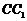 到平面
到平面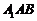 的距離;
的距離;
(Ⅲ)求二面角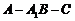 的大小.
的大小.
(1)求證:數列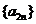 與
與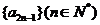 都是等比數列;
都是等比數列;
(2)求數列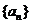 前
前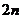 的和
的和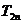 ;
;
(3)若數列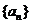 前
前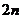 的和為
的和為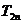 ,不等式
,不等式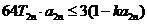 對
對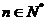 恒成立,求
恒成立,求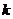 的最大值。
的最大值。
21. (12分)已知函數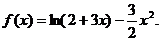
(I)求f(x)在[0,1]上的極值;
(II)若對任意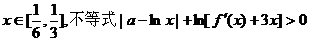 成立,求實數
成立,求實數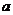 的取值范圍;
的取值范圍;
(III)若關于x的方程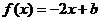 在[0,1]上恰有兩個不同的實根,求實數b的取值范圍.
在[0,1]上恰有兩個不同的實根,求實數b的取值范圍.
22. (14分)已知函數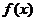 的定義域為
的定義域為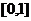 ,且同時滿足:對任意
,且同時滿足:對任意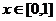 ,總有
,總有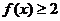 ,
,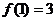 ; 若
; 若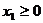 ,
,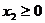 且
且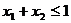 ,則有
,則有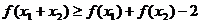 .
.
(I)求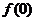 的值;
的值;
(II)試求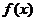 的最大值;
的最大值;
(III)設數列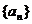 的前
的前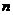 項和為
項和為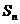 ,且滿足
,且滿足 ,
,
求證: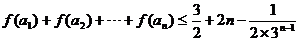 .
.
高2009級一診模擬(理科)數學試題參考解答
一.選擇題:
1.B.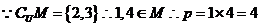
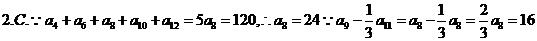
3.D.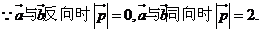
4.B.坐法有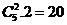
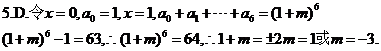
6. A.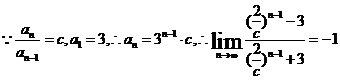
7.D. 由已知得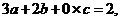 即
即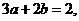
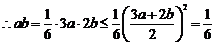
8.C.
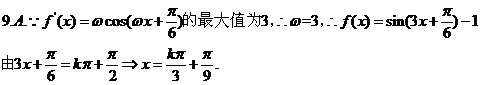
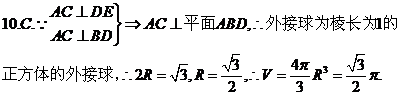
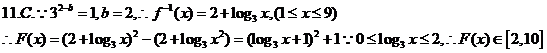
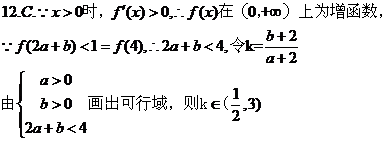
二.填空題:
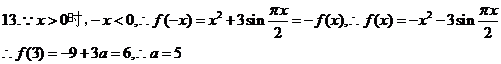
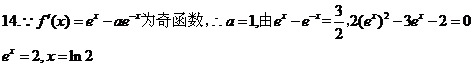
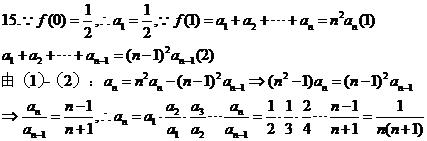
16. ②③.①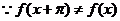 不正確;
不正確;
②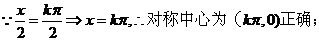
③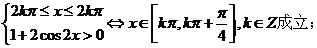
④應按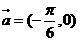 平移,所以不正確.
平移,所以不正確.
三.解答題:
17.解(Ⅰ)由題意知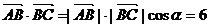
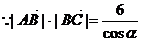
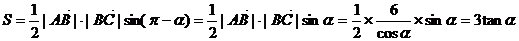
……………………3分
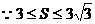
 ……………………4分
……………………4分
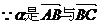 的夾角
的夾角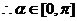
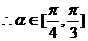 ……………………6分
……………………6分
(Ⅱ)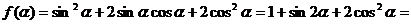
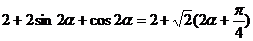 ……………………9分
……………………9分
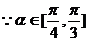
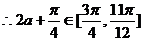
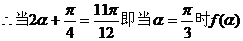 有最小值。
有最小值。
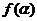 的最小值是
的最小值是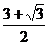 ……………………12分
……………………12分
18.(1)設中國乒乓球男隊獲0枚金牌,女隊獲1枚金牌為事件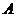 ,中國乒乓球男隊獲1枚金牌,女隊獲2枚金牌為事件
,中國乒乓球男隊獲1枚金牌,女隊獲2枚金牌為事件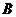 ,那么,
,那么,
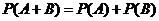 =
=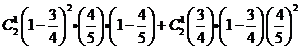 =
=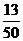
(2)根據題意中國乒乓球隊獲得金牌數是一隨機變量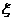 ,它的所有可能取值為0,1,2,3,4(單位:枚)
,它的所有可能取值為0,1,2,3,4(單位:枚)
那么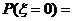
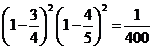
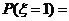
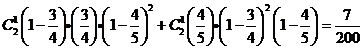
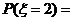
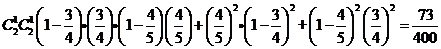
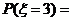
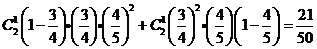
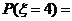
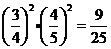 ……………………………………………………(8分)
……………………………………………………(8分)
則概率分布為:
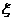
0
1
2
3
4

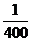
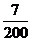
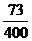
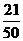
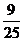
…………………………………………………………………(10分)
那么,所獲金牌的數學期望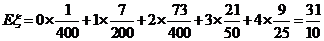 (枚)
(枚)
答:中國乒乓球隊獲得金牌數的期望為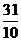 枚。……………………………….(12分)
枚。……………………………….(12分)
19. 解法 :(Ⅰ)∵
:(Ⅰ)∵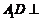 平面
平面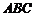 ,∴平面
,∴平面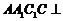 平面
平面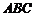 ,
,
又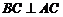 ,∴
,∴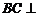 平面
平面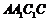 , 得
, 得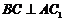 ,又
,又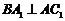 ,
,
 ∴
∴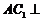 平面
平面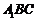 .…………………4分
.…………………4分
(Ⅱ)∵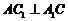 ,四邊形
,四邊形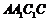 為菱形,故
為菱形,故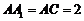 ,
,
又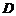 為
為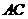 中點,知∴
中點,知∴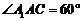 .取
.取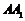 中點
中點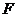 ,則
,則
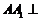 平面
平面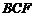 ,從而面
,從而面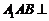 面
面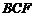 ,…………6分
,…………6分
過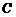 作
作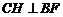 于
于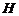 ,則
,則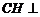 面
面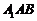 ,在
,在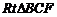 中,
中,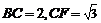 ,故
,故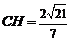 ,即
,即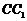 到平面
到平面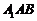 的距離為
的距離為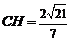 .…………………8分
.…………………8分
(Ⅲ)過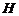 作
作 于
于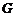 ,連
,連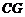 ,則
,則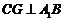 ,從而
,從而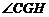 為二面角
為二面角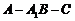 的平面角,在
的平面角,在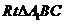 中,
中, ,∴
,∴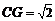 ,…………10分
,…………10分
在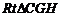 中,
中,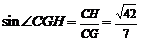 ,故二面角
,故二面角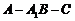 的大小為
的大小為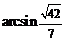 .
.
…………………12分
 解法
解法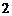 :(Ⅰ)如圖,取
:(Ⅰ)如圖,取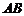 的中點
的中點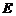 ,則
,則 ,∵
,∵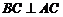 ,∴
,∴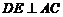 ,
,
又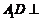 平面
平面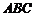 ,以
,以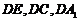 為
為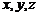 軸建立空間坐標系, …………1分
軸建立空間坐標系, …………1分
則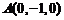 ,
,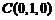 ,
,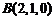 ,
,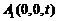 ,
,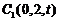 ,
,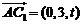 ,
,
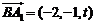 ,
,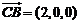 ,由
,由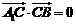 ,知
,知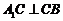 ,
,
又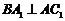 ,從而
,從而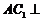 平面
平面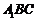 .…………………4分
.…………………4分
(Ⅱ)由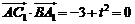 ,得
,得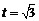 .設平面
.設平面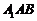 的法向量
的法向量
為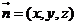 ,
,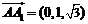 ,
,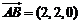 ,
,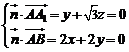 ,
,
設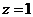 ,則
,則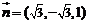 .…………6分
.…………6分
∴點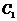 到平面
到平面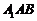 的距離
的距離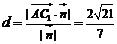 .…………………8分
.…………………8分
(Ⅲ)設面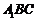 的法向量為
的法向量為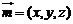 ,
,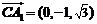 ,
,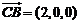 ,
,
∴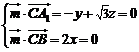 .…………10分
.…………10分
設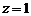 ,則
,則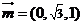 ,故
,故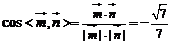 ,根據法向量的方向
,根據法向量的方向
可知二面角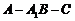 的大小為
的大小為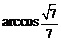 .…………………12分
.…………………12分
20. 解:(1)∵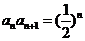 ,∴
,∴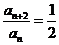 2分
2分
∴數列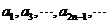 是以1為首項,
是以1為首項,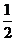 為公比的等比數列;
為公比的等比數列;
(2)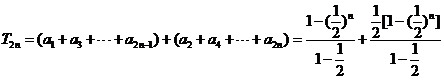
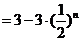 9分
9分
(3)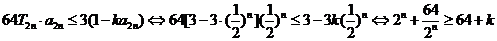
21. 解:(I)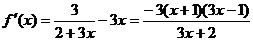 ,
,
令 (舍去)
(舍去)
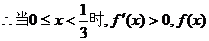 單調遞增;
單調遞增;
當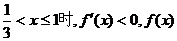 單調遞減.
單調遞減.
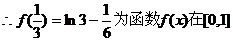 上的極大值
上的極大值
(II)由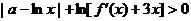 得
得
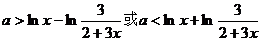 , …………①
, …………①
設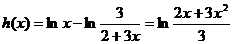 ,
,
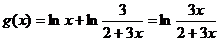 ,
,
依題意知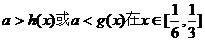 上恒成立,
上恒成立,
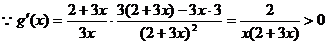 ,
,
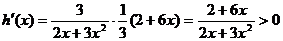 ,
,
 上單增,要使不等式①成立,
上單增,要使不等式①成立,
當且僅當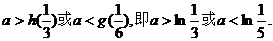
(III)由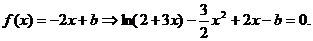
令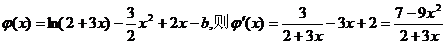 ,
,
當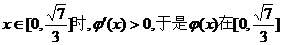 上遞增;
上遞增;
當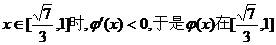 上遞減
上遞減
而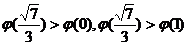 ,
,
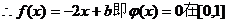 恰有兩個不同實根等價于
恰有兩個不同實根等價于
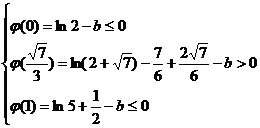
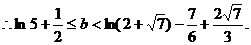
22.解:(1)令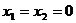 ,則
,則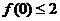 ,又由題意,有
,又由題意,有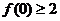
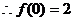 …………………3分
…………………3分
(2)任取 且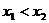 ,則0<
,則0<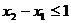
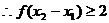
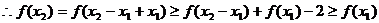
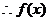 的最大值為
的最大值為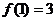 …………………6分
…………………6分
(3)由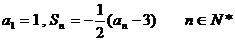
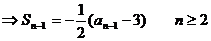
又由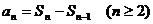
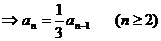
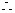 數列
數列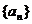 為首項為1,公比為
為首項為1,公比為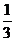 的等比數列,
的等比數列, 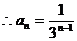 ………8分
………8分
當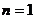 時,
時,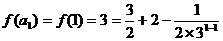 ,不等式成立,
,不等式成立,
當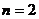 時,
時,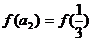
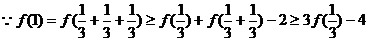 ,
, 
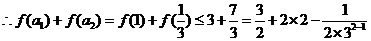 不等式成立
不等式成立
假設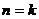 時,不等式成立。
時,不等式成立。
即 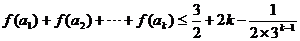
則 當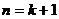 時,
時,
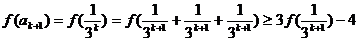
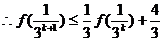
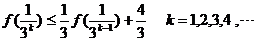
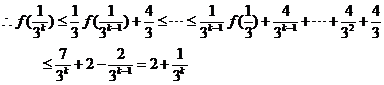
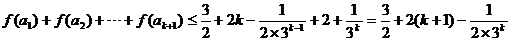
即 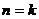 時,不等式成立
時,不等式成立
故
對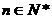 ,原不等式成立。
……………14分
,原不等式成立。
……………14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com