
題目列表(包括答案和解析)
(本小題滿分14分)本題(1)、(2)、(3)三個選答題,每小題7分,任選2題作答,滿分14分,如果多做,則按所做的前兩題計分。作答時,先用2B鉛筆在答題卡上把所選題目對應的題號涂黑,并將所選題號填入括號中。
(1)(本小題滿分7分) 選修4-2:矩陣與變換
已知 ,若
,若 所對應的變換
所對應的變換 把直線
把直線 變換為自身,求實數
變換為自身,求實數 ,并求
,并求 的逆矩陣。
的逆矩陣。
(2)(本題滿分7分)選修4-4:坐標系與參數方程
已知直線 的參數方程:
的參數方程: (
( 為參數)和圓
為參數)和圓 的極坐標方程:
的極坐標方程: 。
。
①將直線 的參數方程化為普通方程,圓
的參數方程化為普通方程,圓 的極坐標方程化為直角坐標方程;
的極坐標方程化為直角坐標方程;
②判斷直線 和圓
和圓 的位置關系。
的位置關系。
(3)(本題滿分7分)選修4-5:不等式選講
已知函數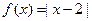
①解不等式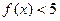 ;
;
②證明:對任意 ,不等式
,不等式 成立.
成立.
(本小題滿分14分)本題(1)、(2)、(3)三個選答題,每小題7分,任選2題作答,滿分14分,如果多做,則按所做的前兩題計分。作答時,先用2B鉛筆在答題卡上把所選題目對應的題號涂黑,并將所選題號填入括號中。
(1)(本小題滿分7分) 選修4-2:矩陣與變換
已知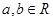 ,若
,若 所對應的變換
所對應的變換 把直線
把直線 變換為自身,求實數
變換為自身,求實數 ,并求
,并求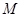 的逆矩陣。
的逆矩陣。
(2)(本題滿分7分)選修4-4:坐標系與參數方程
已知直線 的參數方程:
的參數方程: (
( 為參數)和圓
為參數)和圓 的極坐標方程:
的極坐標方程: 。
。
①將直線 的參數方程化為普通方程,圓
的參數方程化為普通方程,圓 的極坐標方程化為直角坐標方程;
的極坐標方程化為直角坐標方程;
②判斷直線 和圓
和圓 的位置關系。
的位置關系。
(3)(本題滿分7分)選修4-5:不等式選講
已知函數
①解不等式 ;
;
②證明:對任意 ,不等式
,不等式 成立.
成立.
設曲線 :
: 上的點
上的點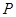 到點
到點 的距離的最小值為
的距離的最小值為 ,若
,若 ,
, ,
,
(1)求數列 的通項公式;
的通項公式;
(2)求證: ;
;
(3)是否存在常數 ,使得對
,使得對 ,都有不等式:
,都有不等式: 成立?請說明理由.
成立?請說明理由.
(本小題滿分12分,(1)小問6分,(2)小分6分.)
設二次函數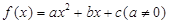 滿足
滿足 ,
,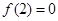 ,且方程
,且方程
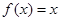 有等根.(1)求
有等根.(1)求 的解析式;
的解析式;
(2)若對一切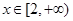 有不等式
有不等式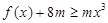 成立,求實數
成立,求實數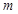 的取值范圍.
的取值范圍.
要證 ,只需證
,只需證 ,即需
,即需 ,即需證
,即需證 ,即證35>11,因為35>11顯然成立,所以原不等式成立。以上證明運用了
,即證35>11,因為35>11顯然成立,所以原不等式成立。以上證明運用了
A.比較法 B.綜合法 C.分析法 D.反證法
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com