
題目列表(包括答案和解析)
同理,當(dāng)a、b都是正實數(shù)時,(a+b)(![]() +
+![]() )≥2ab·2
)≥2ab·2![]() ·
·![]() =4,可以推導(dǎo)出結(jié)論:對于n個正實數(shù)a1,a2,a3,…,an有(a1+a2+a3)(
=4,可以推導(dǎo)出結(jié)論:對于n個正實數(shù)a1,a2,a3,…,an有(a1+a2+a3)(![]() +
+![]() +
+![]() )≥_______;(a1+a2+a3+a4)(
)≥_______;(a1+a2+a3+a4)(![]() +
+![]() +
+![]() +
+![]() )≥________;(a1+a2+a3+…+an)(
)≥________;(a1+a2+a3+…+an)(![]() +
+![]() +
+![]() +···
+···![]() )≥________;
)≥________;
如果對于n個同號實數(shù)a1,a2,a3,…,an(同正或者同負),那么,根據(jù)上述結(jié)論,(a1+a2+a3+…+an)(![]() +
+![]() +
+![]() +···
+···![]() )的取值范圍是________.
)的取值范圍是________.
已知基本不等式:![]() ≥
≥![]() (a、b都是正實數(shù),當(dāng)且僅當(dāng)a=b時等號成立)可以推廣到n個正實數(shù)的情況,即對于n個正實數(shù)a1,a2,a3,…,an,有
(a、b都是正實數(shù),當(dāng)且僅當(dāng)a=b時等號成立)可以推廣到n個正實數(shù)的情況,即對于n個正實數(shù)a1,a2,a3,…,an,有![]() ≥
≥![]() (當(dāng)且僅當(dāng)a1=a2=a3=…=an時,取等號).
(當(dāng)且僅當(dāng)a1=a2=a3=…=an時,取等號).
同理,當(dāng)a、b都是正實數(shù)時,(a+b)(![]() +
+![]() )≥2ab·2
)≥2ab·2![]() ·
·![]() =4,可以推導(dǎo)出結(jié)論:對于n個正實數(shù)a1,a2,a3,…,an有(a1+a2+a3)(
=4,可以推導(dǎo)出結(jié)論:對于n個正實數(shù)a1,a2,a3,…,an有(a1+a2+a3)(![]() +
+![]() +
+![]() )≥________;(a1+a2+a3+a4)(
)≥________;(a1+a2+a3+a4)(![]() +
+![]() +
+![]() +
+![]() )≥________;(a1+a2+a3+…+an)(
)≥________;(a1+a2+a3+…+an)(![]() +
+![]() +
+![]() +…
+…![]() )≥________;
)≥________;
如果對于n個同號實數(shù)a1,a2,a3,…,an(同正或者同負),那么,根據(jù)上述結(jié)論,(a1+a2+a3+…+an)(![]() +
+![]() +
+![]() +…
+…![]() )的取值范圍是________.
)的取值范圍是________.
設(shè)向量 ,
, ,其中
,其中 ,由不等式
,由不等式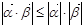 恒成立,可以證明(柯西)不等式
恒成立,可以證明(柯西)不等式 (當(dāng)且僅當(dāng)
(當(dāng)且僅當(dāng) ∥
∥ ,即
,即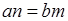 時等號成立),己知
時等號成立),己知 ,若
,若 恒成立,利用可西不等式可求得實數(shù)
恒成立,利用可西不等式可求得實數(shù) 的取值范圍是
的取值范圍是
設(shè)向量 ,
, ,其中
,其中 ,由不等式
,由不等式 恒成立,可以證明(柯西)不等式
恒成立,可以證明(柯西)不等式 (當(dāng)且僅當(dāng)
(當(dāng)且僅當(dāng) ∥
∥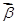 ,即
,即 時等號成立),己知
時等號成立),己知 ,若
,若 恒成立,利用可西不等式可求得實數(shù)
恒成立,利用可西不等式可求得實數(shù) 的取值范圍是
的取值范圍是
設(shè)向量 ,
, ,其中
,其中 ,由不等式
,由不等式 恒成立,可以證明(柯西)不等式
恒成立,可以證明(柯西)不等式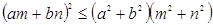 (當(dāng)且僅當(dāng)
(當(dāng)且僅當(dāng) ∥
∥ ,即
,即 時等號成立),己知
時等號成立),己知 ,若
,若 恒成立,利用可西不等式可求得實數(shù)
恒成立,利用可西不等式可求得實數(shù) 的取值范圍是
的取值范圍是
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com