日本成人片在线_久久免费精品视频_国产午夜精品久久久久久免费视_校花撩起jk露出白色内裤国产精品_av影片免费在线观看_国产小视频在线看_最新av免费在线观看_99久久99久久精品国产片_欧美成人猛片aaaaaaa_蜜桃免费网站一区二区三区

21.解：(I)

正面向上次數m	3	2	1	0
概率P(m)

正面向上次數n	2	1	0
概率P(n)

(II)甲獲勝，則m>n,當m=3時，n=2,1,0,其概率為　

　　　　　　　　　　　 當m=2時，n=1,0. 其概率為

　　　　　　　　　　　 當m=1時，n=0　 其概率為　　　

所以，甲獲勝的概率為　　　　　　　　　　

20．解：(I)∵　△為以點M為直角頂點的

等腰直角三角形，

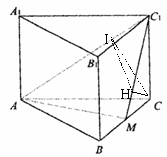∴　且．

∵　正三棱柱，　

∴　底面ABC．

　∴　在底面內的射影為CM，AM⊥CM．

∵　底面ABC為邊長為a的正三角形，　

∴　點M為BC邊的中點．　　　

(II)由(1)知AM⊥且AM⊥CM，∴　AM⊥平面,

　過點C作CH⊥于H，　∵　CH在平面內，　∴　CH⊥AM，

又，有CH⊥平面，

即CH為點C到平面AMC₁的距離

由(1)知，， 且 ．

∴　　　　　　　　　　　　　　　 　∴

∴　點C到平面的距離為底面邊長為．　　　　　　　

(III)過點C作CI⊥于I，連HI，　∵　CH⊥平面，

　∴　HI為CI在平面內的射影，

∴　HI⊥，故∠CIH是二面角的平面角．

在直角三角形中，

，

∴　∠CIH＝45°，　∴　二面角的大小為45°　　

19．解：(1)令紅色球為x個，則依題意得,　 　所以得x=15或x=21，又紅色球多于白色球，所以x=21．所以紅色球為21個，白色球為15個．　　　　　　　　　　　　

(2)設從袋中任取3個小球，至少有一個紅色球的事件為A，均為白色球的事件為B，

則P(B)=1－P(A)＝　＝　　　　

22．如圖正方體在ABCD－A₁B₁C₁D₁中，E，F，G分別為AB，B₁C₁，AA₁的中點，

(1) 求證：EF⊥平面GBD；(2) 求異面直線AD₁與EF所成的角 ．(15分)

21. 甲與乙兩人擲硬幣，甲用一枚硬幣擲3次，記下國徽面(正面)朝上的次數為m，乙用一枚硬幣擲2次，記下國徽面(正面)朝上的次數為n.

(I)填寫下表

(II)規定m>n時甲勝，求甲獲勝的概率。(15分)

20.如圖，正三棱柱的底面邊長為a，點M在邊BC上，△

是以點M為直角頂點的等腰直角三角形．(Ⅰ)求證點M為邊BC的中點；

　(Ⅱ)求點C到平面的距離；(Ⅲ)求二面角的大小。(15分)

19、口袋里裝有紅色和白色共36個不同的球，且紅色球多于白色球．從袋子中取出2個球，若是同色的概率為 ，求：(1) 袋中紅色、白色球各是多少？(2) 從袋中任取3個小球，至少有一個紅色球的概率為多少？(15分)

18. 給四棱錐V-ABCD的五個面涂顏色，要求相鄰的兩個面不得使用同一種顏色，現有4種顏色供選擇，則不同的涂色方法共有　　　　　　　　　 種(以數字作答). ；

17．已知展開式的第四項的值等于10⁶，則x=　　　　

16．的值為　　　　　 2