
【題目】已知x0,x0+![]() 是函數(shù)f(x)=cos2(wx﹣
是函數(shù)f(x)=cos2(wx﹣![]() )﹣sin2wx(ω>0)的兩個相鄰的零點
)﹣sin2wx(ω>0)的兩個相鄰的零點
(1)求![]() 的值;
的值;
(2)若對任意![]() ,都有f(x)﹣m≤0,求實數(shù)m的取值范圍.
,都有f(x)﹣m≤0,求實數(shù)m的取值范圍.
(3)若關(guān)于![]() 的方程
的方程![]() 在
在![]() 上有兩個不同的解,求實數(shù)
上有兩個不同的解,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】試題分析:(1)利用三角恒等變形,對原函數(shù)進行化簡變形,可得![]() ,由兩相鄰零點可得函數(shù)最小正周期,再利用最小正周期與
,由兩相鄰零點可得函數(shù)最小正周期,再利用最小正周期與![]() 的關(guān)系可得函數(shù)表達式,將
的關(guān)系可得函數(shù)表達式,將![]() 代入可得其值;(2)實數(shù)
代入可得其值;(2)實數(shù)![]() 的取值范圍可轉(zhuǎn)化為求函數(shù)
的取值范圍可轉(zhuǎn)化為求函數(shù)![]() 在
在![]() 的最大值問題,利用三角函數(shù)的性質(zhì)可得結(jié)果;(3)類比第二小題,利用分離變量求出
的最大值問題,利用三角函數(shù)的性質(zhì)可得結(jié)果;(3)類比第二小題,利用分離變量求出![]() 的取值范圍,結(jié)合圖象可知與
的取值范圍,結(jié)合圖象可知與![]() 有兩交點時
有兩交點時![]() 的范圍.
的范圍.
試題解析:(1)f(x)= =
=![]()
=![]() =
=![]()
=![]() (
(![]() )=
)=![]() .
.
由題意可知,f(x)的最小正周期T=π,
∴![]() , 又∵ω>0, ∴ω=1,
, 又∵ω>0, ∴ω=1,
∴f(x)=![]() .
.
∴![]() =
=![]() .
.
(2)由f(x)﹣m≤0得,f(x)≤m, ∴m≥f(x)max,
∵﹣![]() , ∴
, ∴![]() , ∴
, ∴![]() ,
,
∴﹣![]() ≤
≤![]() , 即f(x)max=
, 即f(x)max=![]() ,
,
∴![]() 所以
所以![]()
(3)原方程可化為![]()
即![]()
![]()
畫出![]()
![]() 的草圖
的草圖
x=0時,y=2sin![]() =
=![]() ,
,
y的最大值為2,
∴要使方程在x∈[0, ![]() ]上有兩個不同的解,
]上有兩個不同的解,
即![]() ≤m+1<2, 即
≤m+1<2, 即![]() ﹣1≤m<1. 所以
﹣1≤m<1. 所以![]()


 優(yōu)生樂園系列答案
優(yōu)生樂園系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】己知橢圓C:![]() 的左右焦點分別為F1,F(xiàn)2,直線l:y=kx+m與橢圓C交于A,B兩點.O為坐標(biāo)原點.
的左右焦點分別為F1,F(xiàn)2,直線l:y=kx+m與橢圓C交于A,B兩點.O為坐標(biāo)原點.
(1)若直線l過點F1,且|AB|=![]() ,求k的值;
,求k的值;
(2)若以AB為直徑的圓過原點O,試探究點O到直線AB的距離是否為定值?若是,求出該定值;若不是,請說明理由。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線![]() 過定點A,該點也在拋物線
過定點A,該點也在拋物線![]() 上,若拋物線與圓
上,若拋物線與圓![]() 有公共點P,且拋物線在P點處的切線與圓C也相切,則圓C上的點到拋物線的準(zhǔn)線的距離的最小值為__________.
有公共點P,且拋物線在P點處的切線與圓C也相切,則圓C上的點到拋物線的準(zhǔn)線的距離的最小值為__________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】根據(jù)消費者心理學(xué)的研究,商品的銷售件數(shù)與購買人數(shù)存在一定的關(guān)系,商家可以根據(jù)此調(diào)整相應(yīng)的商品小手策略,以謀求商品更多銷量,從而獲取更多利潤.某商場對購買人數(shù)和銷售件數(shù)進行了統(tǒng)計對比,得到如下表格:
人數(shù) | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
件數(shù) | 4 | 7 | 12 | 15 | 20 | 23 | 27 |
(參考公式: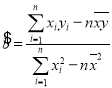 ,
,![]() )
)
(1)以每天進店人數(shù)為橫軸,每天商品銷售件數(shù)為縱軸,畫出散點圖:
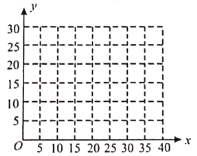
(2)根據(jù)(1)中所繪制的散點圖,可得出購買人數(shù)與商品銷售件數(shù)存在怎樣的關(guān)系?并求出回歸直線方程;(結(jié)果保留到小數(shù)點后兩位)
(3)預(yù)測當(dāng)進店人數(shù)為80人時,商品銷售的件數(shù).(結(jié)果保留整數(shù))
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】將一鐵塊高溫融化后制成一張厚度忽略不計、面積為100dm2的矩形薄鐵皮(如圖),并沿虛線l1,l2裁剪成A,B,C三個矩形(B,C全等),用來制成一個柱體.現(xiàn)有兩種方案:
方案①:以![]() 為母線,將A作為圓柱的側(cè)面展開圖,并從B,C中各裁剪出一個圓形作為圓柱的兩個底面;
為母線,將A作為圓柱的側(cè)面展開圖,并從B,C中各裁剪出一個圓形作為圓柱的兩個底面;
方案②:以![]() 為側(cè)棱,將A作為正四棱柱的側(cè)面展開圖,并從B,C中各裁剪出一個正方形(各邊分別與
為側(cè)棱,將A作為正四棱柱的側(cè)面展開圖,并從B,C中各裁剪出一個正方形(各邊分別與![]() 或
或![]() 垂直)作為正四棱柱的兩個底面.
垂直)作為正四棱柱的兩個底面.
(1)設(shè)B,C都是正方形,且其內(nèi)切圓恰為按方案①制成的圓柱的底面,求底面半徑;
(2)設(shè)![]() 的長為
的長為![]() dm,則當(dāng)
dm,則當(dāng)![]() 為多少時,能使按方案②制成的正四棱柱的體積最大?
為多少時,能使按方案②制成的正四棱柱的體積最大?

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱錐![]() 中,AE垂直于平面
中,AE垂直于平面![]() ,
,![]() ,
,![]() ,點F為平面ABC內(nèi)一點,記直線EF與平面BCE所成角為
,點F為平面ABC內(nèi)一點,記直線EF與平面BCE所成角為![]() ,直線EF與平面ABC所成角為
,直線EF與平面ABC所成角為![]() .
.

![]() Ⅰ
Ⅰ![]() 求證:
求證:![]() 平面ACE;
平面ACE;
![]() Ⅱ
Ⅱ![]() 若
若![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 按如下規(guī)律分布(其中
按如下規(guī)律分布(其中![]() 表示行數(shù),
表示行數(shù),![]() 表示列數(shù)),若
表示列數(shù)),若![]() ,則下列結(jié)果正確的是( )
,則下列結(jié)果正確的是( )
第1列 | 第2列 | 第3列 | 第4列 | … | ||
第1行 | 1 | 3 | 9 | 19 | 33 | |
第2行 | 7 | 5 | 11 | 21 | ||
第3行 | 17 | 15 | 13 | 23 | ||
第4行 | 31 | 29 | 27 | 25 | ||
┇ |
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知平面向量![]() ,
,![]() 滿足:|
滿足:|![]() |=2,|
|=2,|![]() |=1.
|=1.
(1)若(![]() 2
2![]() )(
)(![]() )=1,求
)=1,求![]()
![]() 的值;
的值;
(2)設(shè)向量![]() ,
,![]() 的夾角為θ.若存在t∈R,使得
的夾角為θ.若存在t∈R,使得![]() ,求cosθ的取值范圍.
,求cosθ的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分14分)
已知函數(shù)![]() (
(![]() 為常數(shù))的圖像與
為常數(shù))的圖像與![]() 軸交于點
軸交于點![]() ,曲線
,曲線![]() 在點
在點![]() 處的切線斜率為
處的切線斜率為![]() .
.
(1)求![]() 的值及函數(shù)
的值及函數(shù)![]() 的極值;
的極值;
(2)證明:當(dāng)![]() 時,
時,![]()
(3)證明:對任意給定的正數(shù)![]() ,總存在
,總存在![]() ,使得當(dāng)
,使得當(dāng)![]() 時,恒有
時,恒有![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com