【題目】已知定義在區(qū)間
上的函數(shù)
，
.
（Ⅰ）證明：當(dāng)
時，
；
（Ⅱ）若曲線
過點
的切線有兩條，求實數(shù)
的取值范圍.
【答案】(1)見證明；(2) 
【解析】
（1）利用導(dǎo)數(shù)求得函數(shù)單調(diào)性，可證得
；（2）利用假設(shè)切點的方式寫出切線方程，原問題轉(zhuǎn)化為方程
在
上有兩個解；此時可采用零點存在定理依次判斷零點個數(shù)，得到
范圍，也可以先利用分離變量的方式，構(gòu)造新的函數(shù)，然后討論函數(shù)圖像，得到范圍.
（1）證明：
時，
在
上遞減，在
上遞增
（2）當(dāng)
時，
，
，明顯不滿足要求；
當(dāng)
時，設(shè)切點為
（顯然
），則有
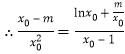，整理得
由題意，要求方程
在區(qū)間上有兩個不同的實數(shù)解
令
①當(dāng)
即
時，
在
上單調(diào)遞增，在
上單調(diào)遞減
或先單調(diào)遞減再遞增
而
，
，
，
在區(qū)間上有唯一零點，在區(qū)間上無零點，
所以此時不滿足題要求.
②當(dāng)
時，
在上單調(diào)遞增
不滿足在區(qū)間上有兩個不同的實數(shù)解
③當(dāng)
即
時，在
上單調(diào)遞增，在
上單調(diào)遞減，在上單調(diào)遞增.
，
在區(qū)間上有唯一零點，所以此時不滿足題要求.
④當(dāng)
時，在上單調(diào)遞減，在上單調(diào)遞增，
，
，
當(dāng)
即
時，在區(qū)間上有唯一零點，此時不滿足題要求.
當(dāng)
即
時，在區(qū)間和上各有一個零點
設(shè)零點為
，又這時
顯然在區(qū)間上單調(diào)遞減
，此時滿足題目要求.
綜上所述，的取值范圍是
（2）解法二：設(shè)切點為
由解法一的關(guān)于
的方程
在區(qū)間內(nèi)有兩解
顯然
不是方程的解
故原問題等價于
在區(qū)間內(nèi)有兩解
設(shè)
，
且
則
，且
令
，，則
又
，
；
，
，
故
，
；
，
從而
，遞增，，遞減
令
， 
由于
時
，時
故，
；，
，
而時，
，
時，
故在區(qū)間內(nèi)有兩解
解得：
名校課堂系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
.
（1）試求函數(shù)
的極值點的個數(shù)；
（2）若
，
恒成立，求
的最大值.
參考數(shù)據(jù)：
| 1.6 | 1.7 | 1.74 | 1.8 | 10 |
| 4.953 | 5.474 | 5.697 | 6.050 | 22026 |
| 0.470 | 0.531 | 0.554 | 0.558 | 2.303 |
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某市春節(jié)期間7家超市的廣告費支出
（萬元）和銷售額
（萬元）數(shù)據(jù)如下：
超市 | A | B | C | D | E | F | G |
廣告費支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
銷售額 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
參數(shù)數(shù)據(jù)及公式：
，
，
，
，
，
，
.
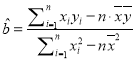（1）若用線性回歸模型擬合y與x的關(guān)系，求y關(guān)于x的線性回歸方程；
（2）用對數(shù)回歸模型擬合y與x的關(guān)系，可得回歸方程：
，經(jīng)計算得出線性回歸模型和對數(shù)模型的
分別約為0.75和0.97，請用說明選擇哪個回歸模型更合適，并用此模型預(yù)測A超市廣告費支出為8萬元時的銷售額.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知
，命題
對任意
，不等式
成立；命題
存在
，使得
成立．
（1）若p為真命題，求m的取值范圍；
（2）若p且q為假，p或q為真，求m的取值范圍；
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在極坐標(biāo)系中，曲線
的方程為
，以極點為原點，極軸所在直線為
軸建立直角坐標(biāo)，直線
的參數(shù)方程為
（
為參數(shù)），與交于
，
兩點．
（1）寫出曲線的直角坐標(biāo)方程和直線的普通方程；
（2）設(shè)點
；若
、
、
成等比數(shù)列，求
的值
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知直線
上有一動點
，過點作直線
垂直于
軸，動點
在上，且滿足
（
為坐標(biāo)原點），記點的軌跡為曲線
.
（1）求曲線的方程；
（2）已知定點
，
，
為曲線上一點，直線
交曲線于另一點
，且點在線段
上，直線
交曲線于另一點
，求
的內(nèi)切圓半徑
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】為了了解一個小水庫中養(yǎng)殖的魚的有關(guān)情況，從這個水庫中多個不同位置捕撈出100條魚，稱得每條魚的質(zhì)量（單位：kg），并將所得數(shù)據(jù)分組，畫出頻率分布直方圖（如圖所示）．
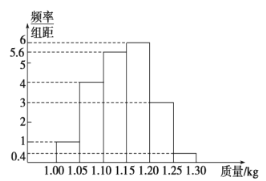
（1）在下面表格中填寫相應(yīng)的頻率；
分組 | 頻率 |
| |
| |
| |
| |
| |
|
（2）估計數(shù)據(jù)落在
中的概率；
（3）將上面捕撈的100條魚分別作一記分組頻率號后再放回水庫．幾天后再從水庫的多處不同位置捕撈出120條魚，其中帶有記號的魚有6條．請根據(jù)這一情況來估計該水庫中魚的總條數(shù)．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在
中，角
，
，
所對的邊分別為
，
，
，且
，則下列結(jié)論正確的是（ ）
A.
B.是鈍角三角形
C.的最大內(nèi)角是最小內(nèi)角的
倍D.若
，則外接圓半徑為
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
