
【題目】已知函數![]() .
.
(1)試求函數![]() 的極值點的個數;
的極值點的個數;
(2)若![]() ,
,![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
參考數據:
| 1.6 | 1.7 | 1.74 | 1.8 | 10 |
| 4.953 | 5.474 | 5.697 | 6.050 | 22026 |
| 0.470 | 0.531 | 0.554 | 0.558 | 2.303 |
【答案】(1)有唯一極小值點,沒有極大值點.(2)10
【解析】
(1)對函數求導可得![]() ,先判斷
,先判斷![]() 在
在![]() 單調遞增,結合
單調遞增,結合![]() 的符號即可得結果;(2)結合(1)中的結論,
的符號即可得結果;(2)結合(1)中的結論,![]() 有唯一極小值點
有唯一極小值點![]() ,故原題等價于
,故原題等價于![]() ,即
,即![]() ,令
,令![]() ,則
,則![]() 在
在![]() 單調遞減,結合表中數據存在唯一正數
單調遞減,結合表中數據存在唯一正數![]() ,使得
,使得![]() ,從而
,從而![]() ,當
,當![]() 時,易知不等式成立,當
時,易知不等式成立,當![]() 時,等價于
時,等價于![]() ,令
,令![]() ,通過導數判斷出
,通過導數判斷出![]() 的單調性,可得
的單調性,可得![]() ,接著證明
,接著證明![]() 時,滿足題意即可.
時,滿足題意即可.
(1)函數![]() 的定義域為
的定義域為![]() ,
,![]() ,
,
當![]() 時,
時,![]() 在
在![]() 單調遞增,
單調遞增,
![]() ,
,![]() 時,
時,![]() ,
,
∴存在唯一正數![]() ,使得
,使得![]() ,
,
函數![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增,
單調遞增,
∴函數![]() 有唯一極小值點
有唯一極小值點![]() ,沒有極大值點,
,沒有極大值點,
∴當![]() 時,
時,![]() 有唯一極小值點,沒有極大值點.
有唯一極小值點,沒有極大值點.
(2)由(1)知,當![]() 時,
時,![]() 有唯一極小值點
有唯一極小值點![]() ,
,
∴![]() ,
,![]() 恒成立
恒成立![]()
![]() ,∴
,∴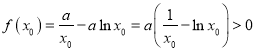 ,
,
∴![]() .
.
令![]() ,則
,則![]() 在
在![]() 單調遞減,
單調遞減,
由于![]() ,
,![]() ,
,
∴存在唯一正數![]() ,使得
,使得![]() ,從而
,從而![]() ,
,
由于![]() 恒成立,
恒成立,
①當![]() 時,
時,![]() 成立;
成立;
②當![]() 時,由于
時,由于![]() ,∴
,∴![]() .
.
令![]() ,當
,當![]() 時,
時,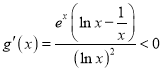 ,
,
∴![]() 在
在![]() 單調遞減,從而
單調遞減,從而![]() .
.
![]() ,且
,且![]() ,且
,且![]() ,
,
∴![]() .
.
下面證明![]() 時,
時,![]() .
.
![]() ,且
,且![]() 在
在![]() 單調遞增,由于
單調遞增,由于![]() ,
,![]() ,
,
∴存在唯一![]() ,使得
,使得![]() ,
,
∴ .
.
令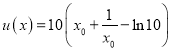 ,
,![]() ,易知
,易知![]() 在
在![]() 單調遞增,
單調遞增,
∴![]() ,
,
∴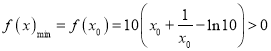 ,即
,即![]() 時,
時,![]() .
.
∴![]() 的最大值是10.
的最大值是10.


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】對于數列![]() ,若存在正數p,使得
,若存在正數p,使得![]() 對任意
對任意![]() 都成立,則稱數列
都成立,則稱數列![]() 為“擬等比數列”.
為“擬等比數列”.
![]() 已知
已知![]() ,
,![]() 且
且![]() ,若數列
,若數列![]() 和
和![]() 滿足:
滿足:![]() ,
,![]() 且
且![]() ,
,![]() .
.
![]() 若
若![]() ,求
,求![]() 的取值范圍;
的取值范圍;
![]() 求證:數列
求證:數列![]() 是“擬等比數列”;
是“擬等比數列”;
![]() 已知等差數列
已知等差數列![]() 的首項為
的首項為![]() ,公差為d,前n項和為
,公差為d,前n項和為![]() ,若
,若![]() ,
,![]() ,
,![]() ,且
,且![]() 是“擬等比數列”,求p的取值范圍
是“擬等比數列”,求p的取值范圍![]() 請用
請用![]() ,d表示
,d表示![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在線段![]() 的兩端點各置一個光源,已知光源
的兩端點各置一個光源,已知光源![]() ,
,![]() 的發光強度之比為
的發光強度之比為![]() ,則線段上光照度最小的一點到
,則線段上光照度最小的一點到![]() ,
,![]() 的距離之比為______(光學定律:
的距離之比為______(光學定律:![]() 點的光照度與
點的光照度與![]() 到光源的距離的平方成反比,與光源的發光強度成正比)
到光源的距離的平方成反比,與光源的發光強度成正比)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 滿足:
滿足:![]() ,
,![]() (其中
(其中![]() 為非零實常數).
為非零實常數).
(1)設![]() ,求證:數列
,求證:數列![]() 是等差數列,并求出通項公式;
是等差數列,并求出通項公式;
(2)設![]() ,記
,記![]() ,求使得不等式
,求使得不等式![]() 成立的最小正整數
成立的最小正整數![]() ;
;
(3)若![]() ,對于任意的正整數
,對于任意的正整數![]() ,均有
,均有![]() ,當
,當![]() 、
、![]() 、
、![]() 依次成等比數列時,求
依次成等比數列時,求![]() 、
、![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】四色猜想是世界三大數學猜想之一,1976年數學家阿佩爾與哈肯證明,稱為四色定理.其內容是:“任意一張平面地圖只用四種顏色就能使具有共同邊界的國家涂上不同的顏色.”用數學語言表示為“將平面任意地細分為不相重疊的區域,每一個區域總可以用![]() ,
,![]() ,
,![]() ,
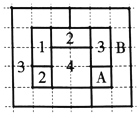
,![]() 四個數字之一標記,而不會使相鄰的兩個區域得到相同的數字.”如圖,網格紙上小正方形的邊長為
四個數字之一標記,而不會使相鄰的兩個區域得到相同的數字.”如圖,網格紙上小正方形的邊長為![]() ,粗實線圍城的各區域上分別標有數字
,粗實線圍城的各區域上分別標有數字![]() ,
,![]() ,
,![]() ,
,![]() 的四色地圖符合四色定理,區域
的四色地圖符合四色定理,區域![]() 和區域
和區域![]() 標記的數字丟失.若在該四色地圖上隨機取一點,則恰好取在標記為
標記的數字丟失.若在該四色地圖上隨機取一點,則恰好取在標記為![]() 的區域的概率所有可能值中,最大的是( )
的區域的概率所有可能值中,最大的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖已知橢圓的焦點在![]() 軸上,其離心率為
軸上,其離心率為![]() ,點
,點![]() 在橢圓上.
在橢圓上.
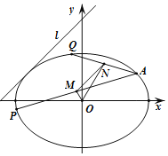
(1)求橢圓的標準方程;
(2)橢圓的弦![]() ,
,![]() 的中點分別為
的中點分別為![]() ,
,![]() ,若
,若![]() 平行于
平行于![]() ,直線
,直線![]() 與橢圓相切,且斜率為1,則
與橢圓相切,且斜率為1,則![]() ,
,![]() 斜率之和是否為定值?若是定值,請求出該定值;若不是定值請說明理由.
斜率之和是否為定值?若是定值,請求出該定值;若不是定值請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l的參數方程為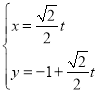 (t為參數),以原點O為極點,x正半軸為極軸建立極坐標系,曲線的極坐標方程為
(t為參數),以原點O為極點,x正半軸為極軸建立極坐標系,曲線的極坐標方程為![]() .
.
(1)求直線l的普通方程和曲線C的直角坐標方程;
(2)設P(0,-1),直線l與C的交點為M,N,線段MN的中點為Q,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題:
①命題“若![]() ,則
,則![]() ”的否命題為“若
”的否命題為“若![]() ,則
,則![]() ”;②“
”;②“![]() ”是“
”是“![]() ”的必要不充分條件;③命題“
”的必要不充分條件;③命題“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ,均有
,均有![]() ”;④命題“若
”;④命題“若![]() ,則
,則![]() ”的逆命題為真命題.其中所有正確命題的序號是_________.
”的逆命題為真命題.其中所有正確命題的序號是_________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com