Question

【題目】如圖,多面體ABCDE中，四邊形ABED是直角梯形，∠BAD=90°，DE∥AB，△ACD是的正三角形，CD=AB=DE=1，BC=

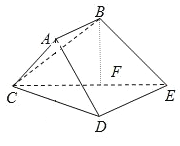
（1）求證：△CDE是直角三角形

（2） F是CE的中點，證明：BF⊥平面CDE

Answer 1

【答案】（1）見解析；（2）見解析

【解析】

(1)根據勾股定理先證明AB⊥AC，結合AB⊥AD，即可證出AB⊥平面ACD，又DE∥AB所以DE⊥平面ACD，即可證明△CDE是直角三角形.

(2) 取CD中點M，連接AM、MF. 先證出MF⊥平面ACD即可得平面CDE⊥平面ACD，利用面面垂直的性質定理可證得AM⊥面CDE，又AM∥BF，即可證出BF⊥平面CDE.

（1）證明：∵∠BAD=90°∴AB⊥AD

△ACD是的正三角形，CD=AB=1，BC=，

∴△ABC是直角三角形，AB⊥AC

∴AB⊥平面ACD

∵DE∥AB

∴DE⊥平面ACD

∴△CDE是直角三角形

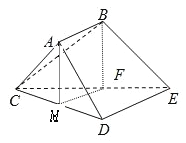
(2)證明:取CD中點M，連接AM、MF.

∵F是CE的中點

∴AMFB是平行四邊形

∴MF∥AB，AM∥BF

∴MF⊥平面ACD

∵MF在平面ECD內

∴平面CDE⊥平面ACD

∵△ACD是的正三角形，M是CD中點

∴AM⊥CD

平面CED∩平面ACD=CD,∴AM⊥面CDE，

∵AM∥BF，

∴BF⊥平面CDE