
【題目】某機械租賃公司有同一型號的機械設備40套,經過一段時間的經營發現:當每套機械設備的月租金為270元時,恰好全部租出,在此基礎上,當每套設備的月租金提高10元時,這種設備就少租一套,且未租出一套設備每月需要支出費用(維護費、管理費等)20元.
(1)設每套設備的月租金為![]() (元),用含
(元),用含![]() 的代數式表示未租出的設備數(套)以及所有未租出設備(套)的支出費用;
的代數式表示未租出的設備數(套)以及所有未租出設備(套)的支出費用;
(2)租賃公司的月收益能否達到11040元?此時應該出租多少套機械設備?每套月租金是多少元?請簡要說明理由;
(3)租賃公司的月收益能否在11040元基礎上再提高?為什么?
【答案】(1)未租出的設備為![]() 套,所有未租出設備的支出費用為
套,所有未租出設備的支出費用為![]() 元;(2)當月租金300元,租出37套;或月租金350元,租出32套,該公司的月收益為11040元,理由見解析;(3)可獲得比11040元更高的月收益,理由見解析
元;(2)當月租金300元,租出37套;或月租金350元,租出32套,該公司的月收益為11040元,理由見解析;(3)可獲得比11040元更高的月收益,理由見解析
【解析】
(1)設每套設備的月租金為![]() (元),則由題意可得到未租出的設備為
(元),則由題意可得到未租出的設備為![]() 套,進而得到所有未租出設備的支出費用;
套,進而得到所有未租出設備的支出費用;
(2)根據題意,列出方程:![]() ,求解后可得;
,求解后可得;
(3)設月收益為![]() 元,根據題意得到二次函數
元,根據題意得到二次函數![]() ,化為頂點式即可得到答案.
,化為頂點式即可得到答案.
(1)設每套設備的月租金為![]() (元),由題意可得未租出的設備為
(元),由題意可得未租出的設備為![]() (套),
(套),
所有未租出設備的支出費用為:![]() 元;
元;
(2)根據題意,列出方程:![]()
解得![]() ,
,![]()
所以當月租金300元,租出37套;或月租金350元,租出32套,該公司的月收益為11040元;
(3)設月收益為![]() 元,根據題意得,
元,根據題意得,![]()
![]() ,
,
即![]() ,
,
當x=325時,y最大為11102.5,則x為325時,租賃公司出租該型號設備的月收益最大,最大月收益為11102.5元.如果按整10元上調價格,則當x=320或330時,最大收益為11100元,收入也大于11040元.
綜上所述,可獲得比11040元更高的月收益.


科目:初中數學 來源: 題型:
【題目】如圖,點P是等邊三角形ABC外接圓⊙O上的點,在以下判斷中,不正確的是

A、當弦PB最長時,ΔAPC是等腰三角形 B、當ΔAPC是等腰三角形時,PO⊥AC
C、當PO⊥AC時,∠ACP=300 D、當∠ACP=300時,ΔPBC是直角三角形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面的圖象反映的過程是:張強從家跑步去體育場,在那里鍛煉了一陣后又原路返回,順路到文具店去買筆,然后散步回家.其中x表示時間,y表示張強離家的距離.根據圖象回答:
(1)體育場離張強家的多遠?張強從家到體育場用了多長時間?
(2)體育場離文具店多遠?
(3)張強在文具店逗留了多久?
(4)計算張強從文具店回家的平均速度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在梯形ABCD中,AD∥BC![]()
![]() ,點E是邊AD的中點,連接BE交AC于F,BE的延長線交CD的延長線于G.
,點E是邊AD的中點,連接BE交AC于F,BE的延長線交CD的延長線于G.
(1)求證:![]() ;
;
(2)若GE=2,BF=3,求線段EF的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC=12厘米,BC=9厘米,點D為AB的中點,如果點P在線段BC上以v厘米/秒的速度由B點向C點運動,同時點Q在線段CA上由C點向A點運動。若點Q的運動速度為3厘米/秒,則當△BPD與△CQP全等時,v的值為_____________
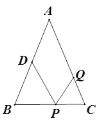
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=﹣![]() x2+bx+c的圖象經過A(2,0),B(0,﹣6)兩點,
x2+bx+c的圖象經過A(2,0),B(0,﹣6)兩點,
(1)求這個二次函數的解析式;
(2)設該二次函數的對稱軸與x軸交于點C,連接BA,BC,求△ABC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在現今“互聯網+”的時代,密碼與我們的生活已經緊密相連,密不可分,而諸如“123456”、生日等簡單密碼又容易被破解,因此利用簡單方法產生一組容易記憶的密碼就很有必要了,有一種用“因式分解”法產生的密碼、方便記憶,其原理是:將一個多項式分解因式,如多項式:![]() 因式分解的結果為
因式分解的結果為![]() ,當
,當![]() 時,
時,![]() 此時可以得到數字密碼171920.
此時可以得到數字密碼171920.
(1)根據上述方法,當![]() 時,對于多項式
時,對于多項式![]() 分解因式后可以形成哪些數字密碼?(寫出三個)
分解因式后可以形成哪些數字密碼?(寫出三個)
(2)若一個直角三角形的周長是24,斜邊長為10,其中兩條直角邊分別為x、y,求出一個由多項式![]() 分解因式后得到的密碼(只需一個即可);
分解因式后得到的密碼(只需一個即可);
(3)若多項式![]() 因式分解后,利用本題的方法,當
因式分解后,利用本題的方法,當![]() 時可以得到其中一個密碼為242834,求m、n的值.
時可以得到其中一個密碼為242834,求m、n的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是“人字形”鋼架,其中斜梁AB=AC,頂角∠BAC=120°,跨度BC=10m,AD為支柱(即底邊BC的中線),兩根支撐架DE⊥AB,DF⊥AC,則DE+DF等于( )

A.10mB.5mC.2.5mD.9.5m
查看答案和解析>>
科目:初中數學 來源: 題型:
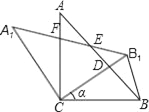
【題目】如圖,△ABC中,∠ACB=90°,AC=BC=1,將△ABC繞點C逆時針旋轉得到△A1B1C,旋轉角為ɑ(0°<ɑ<90°),連接BB1.設CB1交AB于點D,A1B1分別交AB、AC于點E,F.
(1)求證:△BCD≌△A1CF;
(2)若旋轉角ɑ為30°,
①請你判斷△BB1D的形狀;
②求CD的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com