【題目】如圖，在梯形ABCD中，AD∥BC
，點E是邊AD的中點，連接BE交AC于F，BE的延長線交CD的延長線于G.
（1）求證：
；
（2）若GE=2，BF=3，求線段EF的長．
【答案】（1）見解析（2）1.
【解析】
（1）由于AD∥BC，易證得△GED∽△GBC；得GE：GB＝DE：BC；已知AE＝DE，代換相等線段后即可得出本題要證的結論；
（2）按照（1）的方法，可由AE∥BC，得出AE：BC＝EF：FB，再聯立（1）得出的比例關系式，可列出關于EF的方程，即可求得EF的長.
解：（1）證明：
∵AD∥BC，
∠GED＝∠GBC，
∠G＝∠G，
∴△GED∽△GBC，
GE：GB=DE：BC，
∵AE＝DE，
∴EG：GB=AE：BC；
（2）∵AD∥BC，
∴△AEF∽△CBF，
AE：BC=EF：BF，
由(1)問EG：GB=AE：BC，
∴EG：GB=EF：BF，
設EF＝x，
∵GE＝2，BF＝3，
∴x：3=2：(5+x),
x1＝1，x2＝－6（不合題意，舍去）
∴EF＝1．
云南師大附小一線名師提優作業系列答案科目：初中數學 來源： 題型：
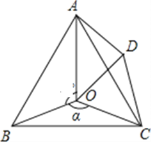
【題目】如圖，點O是等邊△ABC內一點，D是△ABC外的一點，∠AOB=130°，∠BOC=α，△BOC≌△ADC，∠OCD=60°，連接OD．
（1）求證：△OCD是等邊三角形；
（2）當α=150°時，試判斷△AOD的形狀，并說明理由；
（3）探究：當α為多少度時，△AOD是等腰三角形．（直接寫出答案）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知二次函數y=ax2+bx+c的圖象與x軸相交于A（﹣1，0），B（3，0）兩點，與y軸相交于點C（0，﹣3）．
（1）求這個二次函數的表達式；
（2）若P是第四象限內這個二次函數的圖象上任意一點，PH⊥x軸于點H，與BC交于點M，連接PC．
①求線段PM的最大值；
②當△PCM是以PM為一腰的等腰三角形時，求點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，某開發區有一塊四邊形的空地ABCD，現計劃在空地上種植草皮，經測量∠A＝90°，AB＝3m，BC＝12m，CD＝13m，DA＝4m，若每平方米草皮需要200元，則要投入_____元．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，在
中，內角
與外角
的平分線相交于點
，
，
交
于
，交
于
，連接
、
，下列結論：①
；②
；③
垂直平分；④
.其中正確的是（ ）
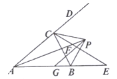
A. ①②④B. ①③④C. ②③④D. ①③
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某機械租賃公司有同一型號的機械設備40套，經過一段時間的經營發現：當每套機械設備的月租金為270元時，恰好全部租出，在此基礎上，當每套設備的月租金提高10元時，這種設備就少租一套，且未租出一套設備每月需要支出費用（維護費、管理費等）20元.
（1）設每套設備的月租金為
（元），用含的代數式表示未租出的設備數（套）以及所有未租出設備（套）的支出費用；
（2）租賃公司的月收益能否達到11040元？此時應該出租多少套機械設備？每套月租金是多少元？請簡要說明理由；
（3）租賃公司的月收益能否在11040元基礎上再提高？為什么？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知△ABC中，AB=AC,把△ABC繞A點沿順時針方向旋轉得到△ADE,聯結BD與CE交于點F，BD交AE于點G.
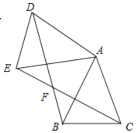
(1)求證:△AEC≌△ADB ;
(2)若AB=2,∠ACB=67.5°，AC∥DF ，求BD的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，二次函數y=﹣
+bx+c的圖象經過點A（1，0），且當x=0和x=5時所對應的函數值相等．一次函數y=﹣x+3與二次函數y=﹣
+bx+c的圖象分別交于B，C兩點，點B在第一象限．
（1）求二次函數y=﹣+bx+c的表達式；
（2）連接AB，求AB的長；
（3）連接AC，M是線段AC的中點，將點B繞點M旋轉180°得到點N，連接AN，CN，判斷四邊形ABCN的形狀，并證明你的結論．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
