
【題目】若二次函數![]() 圖象的頂點在一次函數
圖象的頂點在一次函數![]() 的圖象上,則稱
的圖象上,則稱![]() 為
為![]() 的伴隨函數,如:
的伴隨函數,如:![]() 是
是![]() 的伴隨函數.
的伴隨函數.
(1)若![]() 是
是![]() 的伴隨函數,求直線
的伴隨函數,求直線![]() 與兩坐標軸圍成的三角形的面積;
與兩坐標軸圍成的三角形的面積;
(2)若函數![]() 的伴隨函數
的伴隨函數![]() 與
與![]() 軸兩個交點間的距離為4,求
軸兩個交點間的距離為4,求![]() ,
,![]() 的值.
的值.
【答案】(1)8;(2)![]() ,
,![]() .
.
【解析】
(1)先求出二次函數的頂點,再把頂點代入一次函數求出p,再求出一次函數與坐標軸的交點坐標,再利用三角形的面積公式求解;
(2)先根據函數![]() 與
與![]() 軸兩個交點間的距離為4,求出n,再求出二次函數的頂點,將頂點代入一次函數即可求解.
軸兩個交點間的距離為4,求出n,再求出二次函數的頂點,將頂點代入一次函數即可求解.
解:(1)![]() ,
,
![]() 其頂點坐標為
其頂點坐標為![]() ,
,
![]() 是
是![]() 的伴隨函數,
的伴隨函數,
![]() 在一次函數
在一次函數![]() 的圖象上,
的圖象上,
![]() .
.
![]() ,
,
![]() 一次函數為:
一次函數為:![]() ,
,
![]() 一次函數與坐標軸的交點分別為
一次函數與坐標軸的交點分別為![]() ,
,![]() ,
,
![]() 直線
直線![]() 與兩坐標軸圍成的三角形的兩直角邊長度都為
與兩坐標軸圍成的三角形的兩直角邊長度都為![]() ,
,
![]() 直線
直線![]() 與兩坐標軸圍成的三角形的面積為:
與兩坐標軸圍成的三角形的面積為:![]() .
.
(2)設函數![]() 與
與![]() 軸兩個交點的橫坐標分別為
軸兩個交點的橫坐標分別為![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,
![]() ,
,
∵函數![]() 與
與![]() 軸兩個交點間的距離為4,
軸兩個交點間的距離為4,
![]() ,
,
解得,![]() ,
,
![]() 函數
函數![]() 為:
為:![]() ,
,
![]() 其頂點坐標為
其頂點坐標為![]() ,
,
![]() 是
是![]() 的伴隨函數,
的伴隨函數,
![]() ,
,
![]() .
.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線的頂點為A(1,4),拋物線與y軸交于點B(0,3),與x軸交于C,D兩點.點P是x軸上的一個動點.
(1)求此拋物線的解析式;
(2)當PA+PB的值最小時,求點P的坐標;
(3)拋物線上是否存在一點Q(Q與B不重合),使△CDQ的面積等于△BCD的面積?若存在,直接寫出點Q的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,等腰梯形OABC的底邊OC在x軸上,AB∥OC,O為坐標原點,OA = AB =BC,∠AOC=60°,連接OB,點P為線段OB上一個動點,點E為邊OC中點.
(1)連接PA.PE,求證:PA=PE;
(2)連接PC,若PC+PE=2![]() ,試求AB的最大值;
,試求AB的最大值;
(3)在(2)在條件下,當AB取最大值時,如圖2,點M坐標為(0,-1),點D為線段OC上一個動點,當D點從O點向C點移動時,直線MD與梯形另一邊交點為N,設D點橫坐標為m,當△MNC為鈍角三角形時,求m的范圍.
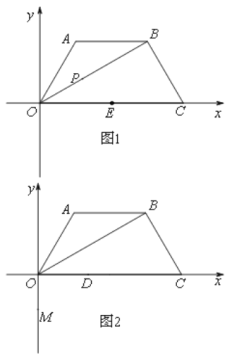
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() ,其對稱軸為直線
,其對稱軸為直線![]() ,結合圖象分析下列結論:①
,結合圖象分析下列結論:①![]() ;②
;②![]() ;③當
;③當![]() 時,
時,![]() 隨
隨![]() 的增大而增大;④一元二次方程
的增大而增大;④一元二次方程![]() 的兩根分別為
的兩根分別為![]() ,
,![]() ;⑤
;⑤![]() ;⑥若
;⑥若![]() ,
,![]() 為方程
為方程![]() 的兩個根,則
的兩個根,則![]() 且
且![]() ,其中正確的結論有( )
,其中正確的結論有( )
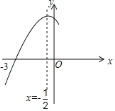
A. ![]() 個B.
個B. ![]() 個C.
個C. ![]() 個D.
個D. ![]() 個
個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】材料1:
經濟學家將家庭或個人在食品消費上的支出與總消費支出的比值稱作恩格爾系數.即:恩格爾系數=![]() ×100%.恩格爾系數可以用來刻劃不同的消費結構,也能間接反映一個國家(地區)不同的發展階段.聯合國糧農組織的規定如表所示:
×100%.恩格爾系數可以用來刻劃不同的消費結構,也能間接反映一個國家(地區)不同的發展階段.聯合國糧農組織的規定如表所示:
恩格爾系數 大于或等于60% | 恩格爾系數 在50%~60%之間 | 恩格爾系數 在40%~50%之間 | 恩格爾系數 在30%~40%之間 | 恩格爾系數 小于30% |
絕對貧困 | 溫 飽 | 小 康 | 富 裕 | 最富裕 |
(注:在50%﹣60%之間是指含50%,不含60% 的所有數據,以此類推)
材料2:
2014年2月22日國家統計局上海調查總隊報道:2013年上海市居民家庭生活消費總支出人均13425元.其中食品支出人均5334元(包括糧食支出450元,蔬菜及制品支出438元,肉禽蛋奶及制品支出1393元,水產品支出581元),衣著支出人均771元,居住支出人均2260元,公用事業支出人均694元,交通通信支出人均1719元,文化教育支出人均964元,醫療保健支出人均1181元,其它支出人均502元.
根據上述材料,
(1)分別計算出“食品”、“衣著”、“居住”、“公用事業”、“交通通信”、“文化教育”和“醫療保健”占家庭生活消費總支出的百分比,并補充完成下列扇形統計圖.(百分號前保留一位小數,圓心角精確到1°)
(2)計算上海市居民的恩格爾系數,并判斷2013年上海市居民的生活水平.
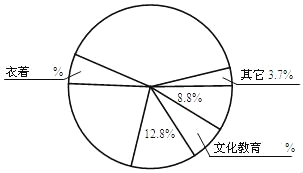
查看答案和解析>>
科目:初中數學 來源: 題型:
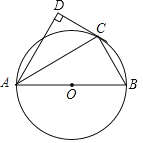
【題目】如圖,AB為⊙O的直徑,點P為AB延長線上的一點,過點P作⊙O的切線PE,切點為M,過A、B兩點分別作PE的垂線AC、BD,垂足分別為C、D,連接AM,則下列結論正確的是___________.(寫出所有正確結論的序號)
①AM平分∠CAB;
②AM2=ACAB;
③若AB=4,∠APE=30°,則![]() 的長為
的長為![]() ;
;
④若AC=3,BD=1,則有CM=DM=![]() .
.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,點D在⊙O外,∠BAD的平分線與⊙O交于點C,連接BC、CD,且∠D=90°.
(1)求證:CD是⊙O的切線;
(2)若∠DCA=60°,BC=3,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC是等邊三角形,AB=![]() ,點D是邊BC上一點,點H是線段AD上一點,連接BH、CH.當∠BHD=60°,∠AHC=90°時,DH=_____.
,點D是邊BC上一點,點H是線段AD上一點,連接BH、CH.當∠BHD=60°,∠AHC=90°時,DH=_____.
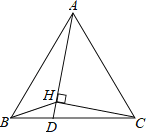
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解不等式組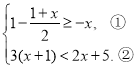
請結合題意填空,完成本題的解答。
(Ⅰ)解不等式①,得_____________;
(Ⅱ)解不等式②,得_____________;
(Ⅲ)把不等式①和②的解集在數軸上表示出來:
![]()
(Ⅳ)原不等式組的解集為_____________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com