
【題目】(1)發現:如圖![]() ,點
,點![]() 是線段
是線段![]() 上的一點,分別以
上的一點,分別以![]() 為邊向外作等邊三角形
為邊向外作等邊三角形![]() 和等邊三角形
和等邊三角形![]() ,連接
,連接![]() ,
,![]() ,相交于點
,相交于點![]() .
.

①線段![]() 與
與![]() 的數量關系為:___________;
的數量關系為:___________;![]() 的度數為__________.
的度數為__________.
②![]() 可看作
可看作![]() 經過怎樣的變換得到的?____________________________.
經過怎樣的變換得到的?____________________________.
(2)應用:如圖![]() ,若點
,若點![]() 不在一條直線上,(1)的結論①還成立嗎?請說明理由;
不在一條直線上,(1)的結論①還成立嗎?請說明理由;
(3)拓展:在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() ,請直接寫出
,請直接寫出![]() ,
,![]() 兩點之間的距離.
兩點之間的距離.
【答案】(1)①![]() ,
,![]() ;(2)依然成立,見解析;(3)
;(2)依然成立,見解析;(3)![]() .
.
【解析】
(1)①證明△ABE≌△CBD,根據全等三角形的性質即可求出線段![]() 與
與![]() 的數量關系;根據三角形外角的性質即可求出
的數量關系;根據三角形外角的性質即可求出![]() 的度數.
的度數.
②根據旋轉的性質即可求解.
(2)根據(1)①中的步驟進行證明即可.
(3)
解:(1)①∵△ABC和△BDE都是等邊三角形,
∴AB=CB,EB=ED,![]()
∴∠ABC+∠CBE=∠DBE+∠CBE,
即∠ABE=∠CBD,
在△ABE和△CBD中,

∴△ABE≌△CBD(SAS),
∴AE=CD,∠BAE=∠BCD,
由三角形的外角性質,∠AOC=∠BAE+∠BDC=∠BCD+∠BDC,
∠ABC=∠BCD+∠BDC,
∴∠AOC=∠ABC=![]() ;
;

故答案為:![]() ;
;![]() .
.
②![]() 可看作由
可看作由![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 得到的(或
得到的(或![]() 可看作由
可看作由![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到)
得到)
(2)依然成立,理由如下:
∵![]() 和
和![]() 均是等邊三角形,
均是等邊三角形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
即![]()
在![]() 和
和![]() 中,
中,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]()
∴![]() .
.
設![]() 與
與![]() 交于點
交于點![]()
∵![]() ,
,
∴![]()
在![]() 和
和![]() 中,其內角和均為
中,其內角和均為![]()
∵![]() ,
,
∴![]()
(3)將![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 得到
得到![]() ,
,
根據旋轉的性質可得:![]()
![]()
![]()
![]()
![]()

![]()


科目:初中數學 來源: 題型:
【題目】省射擊隊為從甲、乙兩名運動員中選拔一人參加全國比賽,對
他們進行了六次測試,測試成績如下表(單位:環):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根據表格中的數據,計算出甲的平均成績是 環,乙的平均成績是 環;
(2)分別計算甲、乙六次測試成績的方差;
(3)根據(1)、(2)計算的結果,你認為推薦誰參加全國比賽更合適,請說明理由.
(計算方差的公式:s2=![]() [
[![]() ])
])
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖①、圖②是兩張形狀和大小完全相同的方格紙,方格紙中每個小正方形的邊長均為1,線段![]() 的兩個端點均在小正方形的頂點上.
的兩個端點均在小正方形的頂點上.

(1)如圖①,點![]() 在小正方形格點上,在圖①中作出點
在小正方形格點上,在圖①中作出點![]() 關于直線
關于直線![]() 的對稱點
的對稱點![]() ,連接
,連接![]() 、
、![]() 、
、![]() 、
、![]() ,并直接寫出四邊形
,并直接寫出四邊形![]() 的周長;
的周長;
(2)在圖②中畫出一個以線段![]() 為一條對角線、面積為15的菱形
為一條對角線、面積為15的菱形![]() ,且點
,且點![]() 和點
和點![]() 均在小正方形的頂點上.
均在小正方形的頂點上.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=kx+b經過點A(-5,0),B(-1,4)
(1)求直線AB的表達式;
(2)求直線CE:y=-2x-4與直線AB及y軸圍成圖形的面積;
(3)根據圖象,直接寫出關于x的不等式kx+b>-2x-4的解集.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,且AB =6,C是⊙O上一點,D是![]() 的中點,過點D作⊙O的切線,與AB、AC的延長線分別交于點E、F,連接AD.
的中點,過點D作⊙O的切線,與AB、AC的延長線分別交于點E、F,連接AD.
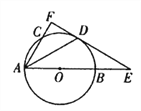
(l)求證:AF⊥EF;
(2)填空:
①當BE= 時,點C是AF的中點;
②當BE= 時,四邊形OBDC是菱形,
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠1=∠2,AB=AD,點E在邊BC上,∠C=∠AED,AB與DE交于點O.

(1)求證:△ABC≌△ADE;
(2)當∠1=40°時,求∠BED的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,小慧從A處出發沿北偏東60°方向行走至B處,又沿北偏西20°方向行走至C處,此時需要將方向調整到與出發時一致,則方向的調整應為( )

A.左轉80°B.右轉80°C.左轉100°D.右轉100°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠ABC=90°,點D,F分別是AC,AB的中點,CE∥DB,BE∥DC.
(1)求證:四邊形DBEC是菱形;
(2)若AD=3,DF=1,求四邊形DBEC面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com