
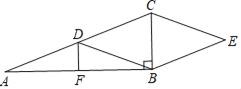
【題目】如圖,Rt△ABC中,∠ABC=90°,點D,F分別是AC,AB的中點,CE∥DB,BE∥DC.
(1)求證:四邊形DBEC是菱形;
(2)若AD=3,DF=1,求四邊形DBEC面積.

【答案】(1)見解析;(2)4![]()
【解析】分析:(1)根據平行四邊形的判定定理首先推知四邊形DBEC為平行四邊形,然后由直角三角形斜邊上的中線等于斜邊的一半得到其鄰邊相等:CD=BD,得證;
(2)由三角形中位線定理和勾股定理求得AB邊的長度,然后根據菱形的性質和三角形的面積公式進行解答.
詳解:(1)證明:∵CE∥DB,BE∥DC,
∴四邊形DBEC為平行四邊形.
又∵Rt△ABC中,∠ABC=90°,點D是AC的中點,
∴CD=BD=![]() AC,
AC,
∴平行四邊形DBEC是菱形;
(2)∵點D,F分別是AC,AB的中點,AD=3,DF=1,
∴DF是△ABC的中位線,AC=2AD=6,S△BCD=![]() S△ABC
S△ABC
∴BC=2DF=2.
又∵∠ABC=90°,
∴AB=![]() =
=![]() =4
=4![]() .
.
∵平行四邊形DBEC是菱形,
∴S四邊形DBEC=2S△BCD=S△ABC=![]() ABBC=
ABBC=![]() ×4
×4![]() ×2=4
×2=4![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖A在數軸上所對應的數為﹣2.
(1)點B在點A右邊距A點4個單位長度,求點B所對應的數;
(2)在(1)的條件下,點A以每秒2個單位長度沿數軸向左運動,點 B 以每秒2個單位長度沿數軸向右運動,當點A運動到﹣6所在的點處時,求A,B兩點間距離.
(3)在(2)的條件下,現A點靜止不動,B點再以每秒2個單位長度沿數軸向左運動時,經過多長時間A,B兩點相距4個單位長度.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以△ABC的三邊為邊分別作等邊△ACD、△ABE、△BCF, 則下列結論:
①△EBF≌△DFC;
②四邊形AEFD為平行四邊形;
③當AB=AC,∠BAC=1200時,四邊形AEFD是正方形.
其中正確的結論是 .(請寫出正確結論的番號).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,點E在邊AD上,點F在邊BC的延長線上,連結EF與邊CD相交于點G,連結BE與對角線AC相交于點H,AE=CF,BE=EG.

(1)求證:EF∥AC;
(2)求∠BEF大小;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB∥DE,AC∥DF,AC=DF,添加下列條件,不能判斷 △ABC≌△DEF的是( )
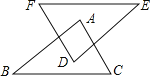
A. EF=BC B. AB=DE C. EF∥BC D. ![]() B=
B=![]() E
E
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,港口A在觀測站O的正東方向,OA=6km,某船從港口A出發,沿北偏東15°方向航行一段距離后到達B處,此時從觀測站O處測得該船位于北偏東60°的方向,則該船航行的距離(即AB的長)為( )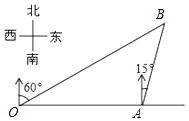
A.3 ![]() km
km
B.3 ![]() km
km
C.4 km
D.(3 ![]() ﹣3)km
﹣3)km
查看答案和解析>>
科目:初中數學 來源: 題型:
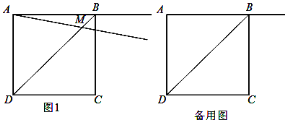
【題目】正方形ABCD的邊長為2,過點A作射線AM與線段BD交于點M,∠BAM=α(0°<α<90°),作CE⊥AM于點E,點N與點M關于直線CE對稱,連接CN.
(1)如圖①,當0°<α<45°時,
①依題意在圖①中補全圖并證明:AM=CN ②當BD∥CN,求DM的值
(2)探究∠NCE與∠BAM之間的數量關系并加以證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探究多邊形內角和問題.
連接多邊形不相鄰的兩個頂點的線段叫做多邊形的對角線.從多邊形某一個頂點出發的×對角線可以把一個多邊形分成幾個三角形.這樣就把多邊形內角和問題轉化為三角形內角和問題了.
(1)請你試一試,做一做,把下面表格補充完整:
名稱 | 圖形 | 內角和 |
三角形 |
| 180° |
四邊形 |
| 2×180°=360° |
五邊形 |
|
|
六邊形 |
|
|
… | … | … |
根據表格探究發現的規律,完成下面的問題:
(2)七邊形的內角和等于 度;
(3)如果一個多邊形有n條邊,請你用含有n的代數式表示這個多邊形的內角和: .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若順次連接四邊形的各邊中點所得的四邊形是菱形,則該四邊形一定是( )
A. 矩形 B. 一組對邊相等,另一組對邊平行的四邊形
C. 對角線互相垂直的四邊形 D. 對角線相等的四邊形
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com