
【題目】己知函數(shù)![]()
![]() .
.
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若函數(shù)![]() 有兩個零點
有兩個零點![]() ,
,![]() ,求
,求![]() 的取值范圍,并證明
的取值范圍,并證明![]() .
.
【答案】(1)見解析;(2)見證明
【解析】
(1)函數(shù)f(x)的定義域為(0,+∞),f′(x)![]() ,x>0,利用分類討論思想,結合導數(shù)性質能討論函數(shù)f(x)的單調(diào)性.
,x>0,利用分類討論思想,結合導數(shù)性質能討論函數(shù)f(x)的單調(diào)性.
(2)先求k的取值范圍是![]() ,再證明f(﹣2k)=ln(﹣2k)
,再證明f(﹣2k)=ln(﹣2k)![]() 0.然后證明x1+x2≥2
0.然后證明x1+x2≥2![]() ,即證(
,即證(![]() 1)(1+t)2<﹣8lnt,即證8lnt+(
1)(1+t)2<﹣8lnt,即證8lnt+(![]() )(1+t)2<0,(t>0).設h(t)=8lnt+(
)(1+t)2<0,(t>0).設h(t)=8lnt+(![]() )(1+t)2,t>1.則h(t)=8lnt﹣t2﹣2t
)(1+t)2,t>1.則h(t)=8lnt﹣t2﹣2t![]() ,t>1.由此能證明x1+x2>2
,t>1.由此能證明x1+x2>2![]() .
.
(1)解:因為![]() ,函數(shù)
,函數(shù)![]() 的定義域為
的定義域為![]() ,
,
所以![]() .
.
當![]() 時,
時,![]() ,
,
所以函數(shù)![]() 在
在![]() 上單調(diào)遞增.
上單調(diào)遞增.
當![]() 時,由
時,由![]() ,得
,得![]() (負根舍去),
(負根舍去),
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
所以函數(shù)![]() 在
在![]() 上單調(diào)遞減;在
上單調(diào)遞減;在![]() 上單調(diào)遞增.
上單調(diào)遞增.
綜上所述,當![]() 時,函數(shù)
時,函數(shù)![]() 在
在![]() 上單調(diào)遞增;當
上單調(diào)遞增;當![]() 時,函數(shù)
時,函數(shù)![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增
上單調(diào)遞增
(2)先求![]() 的取值范圍:
的取值范圍:
方法1:由(1)知,當![]() 時,
時,![]() 在
在![]() 上單調(diào)遞增,不可能有兩個零點,不滿足條件.
上單調(diào)遞增,不可能有兩個零點,不滿足條件.
當![]() 時,函數(shù)
時,函數(shù)![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增,
上單調(diào)遞增,
所以![]() ,
,
要使函數(shù)![]() 有兩個零點,首先
有兩個零點,首先![]() ,解得
,解得![]() .
.
因為![]() ,且
,且![]() ,
,
下面證明![]() .
.
設![]() ,則
,則![]() .
.
因為![]() ,所以
,所以![]() .
.
所以![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
所以![]()
![]() .
.
所以![]() 的取值范圍是
的取值范圍是![]() .
.
方法2:由![]() ,得到
,得到![]() .
.
設![]() ,則
,則![]() .
.
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
所以函數(shù)![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增.
上單調(diào)遞增.
所以由![]()
![]() .
.
因為![]() 時,
時,![]() ,且
,且![]() ,
,
要使函數(shù)![]() 有兩個零點,必有
有兩個零點,必有![]() .
.
所以![]() 的取值范圍是
的取值范圍是![]() .
.
再證明![]() :
:
方法1:因為![]() ,
,![]() 是函數(shù)
是函數(shù)![]() 的兩個零點,不妨設
的兩個零點,不妨設![]() ,令
,令![]() ,則
,則![]() .
.
所以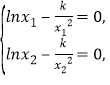 即
即![]() .
.
所以![]() ,即
,即![]() ,
,![]() ,
,![]() .
.
要證![]() ,即證
,即證![]() .
.
即證![]() ,即證
,即證![]() .
.
因為![]() ,所以即證
,所以即證![]() ,
,
或證![]()
![]() .
.
設![]() ,
,![]() .
.
即![]() ,
,![]() .
.
所以![]() .
.
所以![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
所以![]() .
.
所以![]() .
.
方法2:因為![]() ,
,![]() 是函數(shù)
是函數(shù)![]() 有兩個零點,不妨設
有兩個零點,不妨設![]() ,令
,令![]() ,則
,則![]() .
.
所以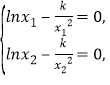 即
即![]() .
.
所以![]() ,即
,即![]() ,
,![]() ,
,![]() .
.
要證![]() ,需證
,需證![]() .
.
即證![]() ,即證
,即證![]() .
.
因為![]() ,所以即證
,所以即證![]()
![]() .
.
設![]() ,
,
則![]() ,
,![]() .
.
所以![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
所以![]()
![]() .
.
所以![]() .
.
方法3:因為![]() ,
,![]() 是函數(shù)
是函數(shù)![]() 有兩個零點,不妨設
有兩個零點,不妨設![]() ,令
,令![]() ,則
,則![]() .
.
所以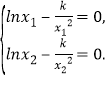 即
即![]() .
.
要證![]() ,需證
,需證![]() .
.
只需證![]() .
.
即證![]() ,即證
,即證![]() .
.
即證![]() .
.
因為![]() ,所以
,所以![]() ,即
,即![]() .
.
所以![]() .
.
而![]() ,
,
所以![]() 成立.
成立.
所以![]() .
.
方法4:因為![]() ,
,![]() 是函數(shù)
是函數(shù)![]() 有兩個零點,不妨設
有兩個零點,不妨設![]() ,令
,令![]() ,則
,則![]() .
.
由已知得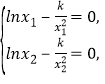 即
即![]() .
.
先證明![]() ,即證明
,即證明![]()
![]() .
.
設![]() ,則
,則![]() .
.
所以![]() 在
在![]() 上單調(diào)遞增,所以
上單調(diào)遞增,所以![]() ,所證不等式成立.
,所證不等式成立.
所以有![]()
![]() .
.
即![]() .
.
因為![]() (
(![]() ),
),
所以![]() ,即
,即![]() .
.
所以![]() .
.
方法5:要證![]() ,其中
,其中![]()
![]() ,
,![]()
![]() ,
,
即證![]() .
.
利用函數(shù)![]() 的單調(diào)性,只需證明
的單調(diào)性,只需證明![]() .
.
因為![]() ,所以只要證明
,所以只要證明![]() ,其中
,其中![]()
![]() .
.
構造函數(shù)![]() ,
,![]() ,
,
則![]() .
.
因為![]()
![]() (利用均值不等式)
(利用均值不等式)
![]()
![]() ,
,
所以![]() 在
在![]()


科目:高中數(shù)學 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為梯形,
為梯形,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)設![]() 為
為![]() 上一點,滿足
上一點,滿足![]() ,若直線
,若直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知四棱錐![]() 的底面為直角梯形,
的底面為直角梯形,![]() ,
,![]() °,
°,![]() 底面
底面![]() ,且
,且![]() ,
,![]() 是
是![]() 的中點.
的中點.

(1)證明:平面![]() 平面
平面![]() ;
;
(2)求![]() 與
與![]() 所成角的余弦值;
所成角的余弦值;
(3)求平面![]() 與平面
與平面![]() 所成二面角(銳角)的余弦值.
所成二面角(銳角)的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系![]() 中,傾斜角為
中,傾斜角為![]() 的直線
的直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)).在以坐標原點為極點,
為參數(shù)).在以坐標原點為極點,![]() 軸正半軸為極軸的極坐標系中,曲線
軸正半軸為極軸的極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的傾斜角.
的傾斜角.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】科研人員在對人體脂肪含量和年齡之間關系的研究中,獲得了一些年齡和脂肪含量的簡單隨機樣本數(shù)據(jù),如下表:
| 26 | 27 | 39 | 41 | 49 | 53 | 56 | 58 | 60 | 61 |
| 14.5 | 17.8 | 21.2 | 25.9 | 26.3 | 29.6 | 31.4 | 33.5 | 35.2 | 34.6 |
根據(jù)上表的數(shù)據(jù)得到如下的散點圖.
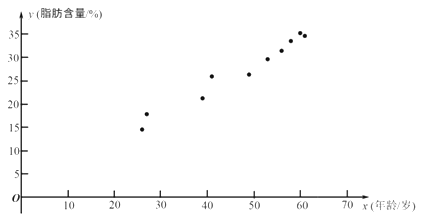
(1)根據(jù)上表中的樣本數(shù)據(jù)及其散點圖:
(i)求![]() ;
;
(i)計算樣本相關系數(shù)(精確到0.01),并刻畫它們的相關程度.
(2)若![]() 關于
關于![]() 的線性回歸方程為
的線性回歸方程為![]() ,求
,求![]() 的值(精確到0.01),并根據(jù)回歸方程估計年齡為50歲時人體的脂肪含量.
的值(精確到0.01),并根據(jù)回歸方程估計年齡為50歲時人體的脂肪含量.
附:參考數(shù)據(jù):img src="http://thumb.zyjl.cn/Upload/2019/08/18/08/786210e5/SYS201908180802150104289801_ST/SYS201908180802150104289801_ST.007.png" width="51" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
參考公式:相關系數(shù)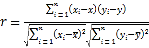
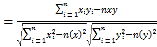
回歸方程![]() 中斜率和截距的最小二乘估計公式分別為
中斜率和截距的最小二乘估計公式分別為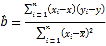 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】正三棱柱![]() 的底面邊長是2,側棱長是4,
的底面邊長是2,側棱長是4,![]() 是
是![]() 的中點.
的中點.![]() 是
是![]() 中點,
中點,![]() 是
是![]() 中點,
中點,![]() 是
是![]() 中點,
中點,
(1)計算異面直線![]() 與
與![]() 所成角的余弦值
所成角的余弦值
(2)求證:![]() 平面
平面![]()
(3)求證:面![]() 面
面![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】自貢農(nóng)科所實地考察,研究發(fā)現(xiàn)某貧困村適合種植![]() ,
,![]() 兩種藥材,可以通過種植這兩種藥材脫貧.通過大量考察研究得到如下統(tǒng)計數(shù)據(jù):藥材
兩種藥材,可以通過種植這兩種藥材脫貧.通過大量考察研究得到如下統(tǒng)計數(shù)據(jù):藥材![]() 的畝產(chǎn)量約為300公斤,其收購價格處于上漲趨勢,最近五年的價格如下表:
的畝產(chǎn)量約為300公斤,其收購價格處于上漲趨勢,最近五年的價格如下表:
編號 | 1 | 2 | 3 | 4 | 5 |
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
單價(元/公斤) | 18 | 20 | 23 | 25 | 29 |
藥材![]() 的收購價格始終為20元/公斤,其畝產(chǎn)量的頻率分布直方圖如下:
的收購價格始終為20元/公斤,其畝產(chǎn)量的頻率分布直方圖如下:

(1)若藥材![]() 的單價
的單價![]() (單位:元/公斤)與年份編號
(單位:元/公斤)與年份編號![]() 具有線性相關關系,請求出
具有線性相關關系,請求出![]() 關于
關于![]() 的回歸直線方程,并估計2020年藥材
的回歸直線方程,并估計2020年藥材![]() 的單價;
的單價;
(2)用上述頻率分布直方圖估計藥材![]() 的平均畝產(chǎn)量,若不考慮其他因素,試判斷2020年該村應種植藥材
的平均畝產(chǎn)量,若不考慮其他因素,試判斷2020年該村應種植藥材![]() 還是藥材
還是藥材![]() ?并說明理由.
?并說明理由.
參考公式: ,
,![]() (回歸方程
(回歸方程![]() 中)
中)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】英語老師要求學生從星期一到星期四每天學習3個英語單詞:每周五對一周內(nèi)所學單詞隨機抽取若干個進行檢測(一周所學的單詞每個被抽到的可能性相同)
(1)英語老師隨機抽了![]() 個單詞進行檢測,求至少有
個單詞進行檢測,求至少有![]() 個是后兩天學習過的單詞的概率;
個是后兩天學習過的單詞的概率;
(2)某學生對后兩天所學過的單詞每個能默寫對的概率為![]() ,對前兩天所學過的單詞每個能默寫對的概率為
,對前兩天所學過的單詞每個能默寫對的概率為![]() ,若老師從后三天所學單詞中各抽取一個進行檢測,求該學生能默寫對的單詞的個數(shù)
,若老師從后三天所學單詞中各抽取一個進行檢測,求該學生能默寫對的單詞的個數(shù)![]() 的分布列和期望。
的分布列和期望。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,四個點
中,四個點 ,
, ,
, ,
, 中有3個點在橢圓
中有3個點在橢圓![]() :
:![]() 上.
上.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過原點的直線與橢圓![]() 交于
交于![]() ,
,![]() 兩點(
兩點(![]() ,
,![]() 不是橢圓
不是橢圓![]() 的頂點),點
的頂點),點![]() 在橢圓
在橢圓![]() 上,且
上,且![]() ,直線
,直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于
軸分別交于![]() 、
、![]() 兩點,設直線
兩點,設直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,證明:存在常數(shù)
,證明:存在常數(shù)![]() 使得
使得![]() ,并求出
,并求出![]() 的值.
的值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com