
【題目】如圖所示,該幾何體是由一個直三棱柱![]() 和一個正四棱錐
和一個正四棱錐![]() 組合而成,
組合而成, ![]() ,
, ![]() .
.

(Ⅰ)證明:平面![]() 平面
平面![]() ;
;
(Ⅱ)求正四棱錐![]() 的高
的高![]() ,使得二面角
,使得二面角![]() 的余弦值是
的余弦值是![]() .
.
科目:高中數學 來源: 題型:
【題目】
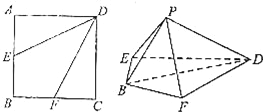
如圖,在正方形ABCD中,點E,F分別是AB,BC的中點.將△AED,△DCF分別沿DE,DF折起,使A,C兩點重合于P.
(1)求證:平面PBD⊥平面BFDE;
(2)求二面角P﹣DE﹣F的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設要抽查某企業生產的某種品牌的袋裝牛奶的質量是否達標,現從700袋牛奶中抽取50袋進行檢驗.利用隨機數表抽取樣本時,先將700袋牛奶按001,002,…,700進行編號,如果從隨機數表第3行第1組數開始向右讀,最先讀到的5袋牛奶的編號是614,593,379,242,203,請你以此方式繼續向右讀數,隨后讀出的3袋牛奶的編號是 . (下列摘取了隨機數表第1行至第5行) 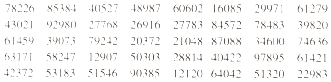
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某學校組織的一次智力競賽中,比賽共分為兩個環節,其中第一環節競賽題有A、B兩組題,每個選手最多有3次答題機會,答對一道A組題得20分,答對一道B組題得30分.選手可以任意選擇答題的順序,如果前兩次得分之和超過30分即停止答題,進入下一環節比賽,否則答3次.某同學正確回答A組題的概率都是p,正確回答B組題的概率都是 ![]() ,且回答正確與否相互之間沒有影響.該同學選擇先答一道B組題,然后都答A組題.已知第一環節比賽結束時該同學得分超過30分的概率為
,且回答正確與否相互之間沒有影響.該同學選擇先答一道B組題,然后都答A組題.已知第一環節比賽結束時該同學得分超過30分的概率為 ![]() .
.
(1)求p的值;
(2)用ξ表示第一環節比賽結束后該同學的總得分,求隨機變量ξ的數學期望;
(3)試比較該同學選擇都回答A組題與選擇上述方式答題,能進入下一環節競賽的概率的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設小明家訂了一份報紙,送報人可能在早上6:30﹣7:30之間把報紙送到小明家,小明父親離開家去工作的時間在早上7:00﹣8:00之間,問小明父親在離開家前能得到報紙(稱為事件A)的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數f(x)=x2+2bx+c(b,c∈R).
(1)若函數y=f(x)的零點為﹣1和1,求實數b,c的值;
(2)若f(x)滿足f(1)=0,且關于x的方程f(x)+x+b=0的兩個實數根分別在區間(﹣3,﹣2),(0,1)內,求實數b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若![]() ,求曲線
,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)若函數![]() 在其定義域內為增函數,求
在其定義域內為增函數,求![]() 的取值范圍;
的取值范圍;
(3)在(2)的條件下,設函數![]() ,若在
,若在![]() 上至少存在一點
上至少存在一點![]() ,使得
,使得![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用數學歸納法證明命題“當n是正奇數時,xn+yn能被x+y整除”,在第二步的證明時,正確的證法是( )
A.假設n=k(k∈N*)時命題成立,證明n=k+1時命題也成立
B.假設n=k(k是正奇數)時命題成立,證明n=k+1時命題也成立
C.假設n=k(k是正奇數)時命題成立,證明n=k+2時命題也成立
D.假設n=2k+1(k∈N)時命題成立,證明n=k+1時命題也成立
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)是定義在R上的奇函數,且當x>0時,f(x)=x2+2x.
(Ⅰ)求f(0)的值;
(Ⅱ)求此函數在R上的解析式;
(Ⅲ)若對任意的t∈R,不等式f(t+1)+f(m﹣2t2)<0恒成立,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com