
【題目】在三棱錐![]() 中,
中,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,點
,點![]() 在棱
在棱![]() 上.
上.
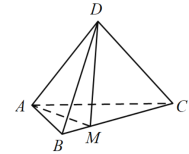
![]() 若
若![]() 為
為![]() 的中點,證明:
的中點,證明:![]() .
.
![]() 若
若![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求
,求![]() .
.
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,曲線C1的參數方程為![]() (
(![]() 為參數),以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,曲線C2的極坐標方程為
為參數),以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,曲線C2的極坐標方程為![]() .
.
(1)寫出曲線C1和C2的直角坐標方程;
(2)已知P為曲線C2上的動點,過點P作曲線C1的切線,切點為A,求|PA|的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在國家批復成立江北新區后,南京市政府規劃在新區內的一條形地塊上新建一個全民健身中心,規劃區域為四邊形ABCD,如圖![]() ,
,![]() ,點B在線段OA上,點C、D分別在射線OP與AQ上,且A和C關于BD對稱.已知
,點B在線段OA上,點C、D分別在射線OP與AQ上,且A和C關于BD對稱.已知![]() .
.
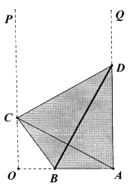
(1)若![]() ,求BD的長;
,求BD的長;
(2)問點C在何處時,規劃區域的面積最小?最小值是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過拋物線![]() 上一點
上一點![]() 作直線交拋物線E于另一點N.
作直線交拋物線E于另一點N.
(1)若直線MN的斜率為1,求線段![]() 的長.
的長.
(2)不過點M的動直線l交拋物線E于A,B兩點,且以AB為直徑的圓經過點M,問動直線l是否恒過定點.如果有求定點坐標,如果沒有請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】廠家在產品出廠前,需對產品做檢驗,第一次檢測廠家的每件產品合格的概率為![]() ,如果合格,則可以出廠;如果不合格,則進行技術處理,處理后進行第二次檢測.每件產品的合格率為
,如果合格,則可以出廠;如果不合格,則進行技術處理,處理后進行第二次檢測.每件產品的合格率為![]() ,如果合格,則可以出廠,不合格則當廢品回收.
,如果合格,則可以出廠,不合格則當廢品回收.
![]() 求某件產品能出廠的概率;
求某件產品能出廠的概率;
![]() 若該產品的生產成本為
若該產品的生產成本為![]() 元/件,出廠價格為
元/件,出廠價格為![]() 元/件,每次檢測費為
元/件,每次檢測費為![]() 元/件,技術處理每次
元/件,技術處理每次![]() 元/件,回收獲利
元/件,回收獲利![]() 元/件.假如每件產品是否合格相互獨立,記
元/件.假如每件產品是否合格相互獨立,記![]() 為任意一件產品所獲得的利潤,求隨機變量
為任意一件產品所獲得的利潤,求隨機變量![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線C的參數方程為
中,曲線C的參數方程為![]() (
(![]() 為參數),以原點O為極點,x軸正半軸為極軸建立極坐標系,直線
為參數),以原點O為極點,x軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() ,且直線
,且直線![]() 與曲線C有兩個不同的交點.
與曲線C有兩個不同的交點.
(1)求實數a的取值范圍;
(2)已知M為曲線C上一點,且曲線C在點M處的切線與直線![]() 垂直,求點M的直角坐標.
垂直,求點M的直角坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某便利店統計了今年第一季度各個品類的銷售收入占比和凈利潤占比,并將部分品類的這兩個數據制成如下統計圖(注:銷售收入占比![]() ,凈利潤占比
,凈利潤占比![]() ,凈利潤
,凈利潤![]() 銷售收入
銷售收入![]() 成本
成本![]() 各類費用),現給出下列判斷:
各類費用),現給出下列判斷:
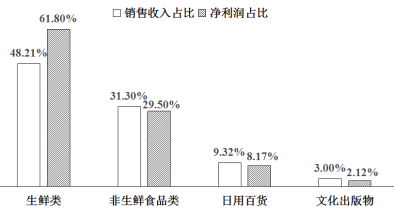
①該便利店第一季度至少有一種品類是虧損的;
②該便利店第一季度的銷售收入中“生鮮類”貢獻最大;
③該便利店第一季度“非生鮮食品類”的凈利潤一定高于“日用百貨”的銷售收入;
④該便利店第一季度“生鮮類”的銷售收入比“非生鮮食品類”的銷售收入多![]() .
.
則上述判斷中正確的是( )
A.①②B.②③C.①④D.③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知點![]() 是
是![]() 軸下方(不含
軸下方(不含![]() 軸)一點,拋物線
軸)一點,拋物線![]() 上存在不同的兩點
上存在不同的兩點![]() 、
、![]() 滿足
滿足![]() ,
,![]() ,其中
,其中![]() 為常數,且
為常數,且![]() 、
、![]() 兩點均在
兩點均在![]() 上,弦
上,弦![]() 的中點為
的中點為![]() .
.
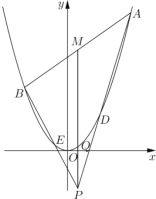
(1)若![]() 點坐標為
點坐標為![]() ,
,![]() 時,求弦
時,求弦![]() 所在的直線方程;
所在的直線方程;
(2)在(1)的條件下,如果過![]() 點的直線
點的直線![]() 與拋物線
與拋物線![]() 只有一個交點,過
只有一個交點,過![]() 點的直線
點的直線![]() 與拋物線
與拋物線![]() 也只有一個交點,求證:若
也只有一個交點,求證:若![]() 和
和![]() 的斜率都存在,則
的斜率都存在,則![]() 與
與![]() 的交點
的交點![]() 在直線
在直線![]() 上;
上;
(3)若直線![]() 交拋物線
交拋物線![]() 于點
于點![]() ,求證:線段
,求證:線段![]() 與
與![]() 的比為定值,并求出該定值.
的比為定值,并求出該定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com