
【題目】某協(xié)會(huì)對(duì)![]() ,
,![]() 兩家服務(wù)機(jī)構(gòu)進(jìn)行滿意度調(diào)查,在
兩家服務(wù)機(jī)構(gòu)進(jìn)行滿意度調(diào)查,在![]() ,
,![]() 兩家服務(wù)機(jī)構(gòu)提供過(guò)服務(wù)的市民中隨機(jī)抽取了
兩家服務(wù)機(jī)構(gòu)提供過(guò)服務(wù)的市民中隨機(jī)抽取了![]() 人,每人分別對(duì)這兩家服務(wù)機(jī)構(gòu)進(jìn)行獨(dú)立評(píng)分,滿分均為
人,每人分別對(duì)這兩家服務(wù)機(jī)構(gòu)進(jìn)行獨(dú)立評(píng)分,滿分均為![]() 分.整理評(píng)分?jǐn)?shù)據(jù),將分?jǐn)?shù)以
分.整理評(píng)分?jǐn)?shù)據(jù),將分?jǐn)?shù)以![]() 為組距分成
為組距分成![]() 組:
組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到
,得到![]() 服務(wù)機(jī)構(gòu)分?jǐn)?shù)的頻數(shù)分布表,
服務(wù)機(jī)構(gòu)分?jǐn)?shù)的頻數(shù)分布表,![]() 服務(wù)機(jī)構(gòu)分?jǐn)?shù)的頻率分布直方圖:
服務(wù)機(jī)構(gòu)分?jǐn)?shù)的頻率分布直方圖:


定義市民對(duì)服務(wù)機(jī)構(gòu)評(píng)價(jià)的“滿意度指數(shù)”如下:
分?jǐn)?shù) |
|
|
|
滿意度指數(shù) | 0 | 1 | 2 |
(1)在抽樣的![]() 人中,求對(duì)
人中,求對(duì)![]() 服務(wù)機(jī)構(gòu)評(píng)價(jià)“滿意度指數(shù)”為
服務(wù)機(jī)構(gòu)評(píng)價(jià)“滿意度指數(shù)”為![]() 的人數(shù);
的人數(shù);
(2)從在![]() ,
,![]() 兩家服務(wù)機(jī)構(gòu)都提供過(guò)服務(wù)的市民中隨機(jī)抽取
兩家服務(wù)機(jī)構(gòu)都提供過(guò)服務(wù)的市民中隨機(jī)抽取![]() 人進(jìn)行調(diào)查,試估計(jì)對(duì)
人進(jìn)行調(diào)查,試估計(jì)對(duì)![]() 服務(wù)機(jī)構(gòu)評(píng)價(jià)的“滿意度指數(shù)”比對(duì)
服務(wù)機(jī)構(gòu)評(píng)價(jià)的“滿意度指數(shù)”比對(duì)![]() 服務(wù)機(jī)構(gòu)評(píng)價(jià)的“滿意度指數(shù)”高的概率;
服務(wù)機(jī)構(gòu)評(píng)價(jià)的“滿意度指數(shù)”高的概率;
(3)如果從![]() ,
,![]() 服務(wù)機(jī)構(gòu)中選擇一家服務(wù)機(jī)構(gòu),以滿意度出發(fā),你會(huì)選擇哪一家?說(shuō)明理由.
服務(wù)機(jī)構(gòu)中選擇一家服務(wù)機(jī)構(gòu),以滿意度出發(fā),你會(huì)選擇哪一家?說(shuō)明理由.
【答案】(1)200;(2)見解析;(3)見解析.
【解析】試題分析:(1)由對(duì)B服務(wù)機(jī)構(gòu)的頻率分布直方圖,得對(duì)B服務(wù)機(jī)構(gòu)“滿意度指數(shù)”為0的頻率為0.2,由此能求出對(duì)B服務(wù)機(jī)構(gòu)評(píng)價(jià)“滿意度指數(shù)”為0的人數(shù);
(2)設(shè)“對(duì)B服務(wù)機(jī)構(gòu)評(píng)價(jià)‘滿意度指數(shù)’比對(duì)A服務(wù)機(jī)構(gòu)評(píng)價(jià)‘滿意度指數(shù)’高”為事件C.記“對(duì)B服務(wù)機(jī)構(gòu)評(píng)價(jià)‘滿意度指數(shù)’為1”為事件B1;“對(duì)B服務(wù)機(jī)構(gòu)評(píng)價(jià)‘滿意度指數(shù)’為2”為事件B2;“對(duì)A服務(wù)機(jī)構(gòu)評(píng)價(jià)‘滿意度指數(shù)’為0”為事件A0;“對(duì)A服務(wù)機(jī)構(gòu)評(píng)價(jià)‘滿意度指數(shù)’為1”為事件A1.P(C)=P(B1A0+B2A0+B2A1),由此能求出該學(xué)生對(duì)B服務(wù)機(jī)構(gòu)評(píng)價(jià)的“滿意度指數(shù)”比對(duì)A服務(wù)機(jī)構(gòu)評(píng)價(jià)的“滿意度指數(shù)”高的概率;
(3)如果從學(xué)生對(duì)A,B兩服務(wù)機(jī)構(gòu)評(píng)價(jià)的“滿意度指數(shù)”的期望角度看分別求出B服務(wù)機(jī)構(gòu)“滿意度指數(shù)”X的分布列和A服務(wù)機(jī)構(gòu)“滿意度指數(shù)”Y的分布列,由此能出結(jié)果.
試題解析:
(1)由對(duì)![]() 服務(wù)機(jī)構(gòu)的頻率分布直方圖,得
服務(wù)機(jī)構(gòu)的頻率分布直方圖,得
對(duì)![]() 服務(wù)機(jī)構(gòu)“滿意度指數(shù)”為0的頻率為
服務(wù)機(jī)構(gòu)“滿意度指數(shù)”為0的頻率為![]() ,
,
所以,對(duì)![]() 服務(wù)機(jī)構(gòu)評(píng)價(jià)“滿意度指數(shù)”為0的人數(shù)為
服務(wù)機(jī)構(gòu)評(píng)價(jià)“滿意度指數(shù)”為0的人數(shù)為![]() 人.
人.
(2)設(shè)“對(duì)![]() 服務(wù)機(jī)構(gòu)評(píng)價(jià)‘滿意度指數(shù)’比對(duì)
服務(wù)機(jī)構(gòu)評(píng)價(jià)‘滿意度指數(shù)’比對(duì)![]() 服務(wù)機(jī)構(gòu)評(píng)價(jià)‘滿意度指數(shù)’高”為事件
服務(wù)機(jī)構(gòu)評(píng)價(jià)‘滿意度指數(shù)’高”為事件![]() .
.
記“對(duì)![]() 服務(wù)機(jī)構(gòu)評(píng)價(jià)‘滿意度指數(shù)’為1”為事件
服務(wù)機(jī)構(gòu)評(píng)價(jià)‘滿意度指數(shù)’為1”為事件![]() ;“對(duì)
;“對(duì)![]() 服務(wù)機(jī)構(gòu)評(píng)價(jià)‘滿意度指數(shù)’為2” 為事件
服務(wù)機(jī)構(gòu)評(píng)價(jià)‘滿意度指數(shù)’為2” 為事件![]() ;“對(duì)
;“對(duì)![]() 服務(wù)機(jī)構(gòu)評(píng)價(jià)‘滿意度指數(shù)’為0”為事件
服務(wù)機(jī)構(gòu)評(píng)價(jià)‘滿意度指數(shù)’為0”為事件![]() ;“對(duì)
;“對(duì)![]() 服務(wù)機(jī)構(gòu)評(píng)價(jià)‘滿意度指數(shù)’為1”為事件
服務(wù)機(jī)構(gòu)評(píng)價(jià)‘滿意度指數(shù)’為1”為事件![]() .
.
所以![]() ,
,
由用頻率估計(jì)概率得:![]() ,
,
因?yàn)槭录?/span>![]() 與
與![]() 相互獨(dú)立,其中
相互獨(dú)立,其中![]() .
.
所以![]()
所以該學(xué)生對(duì)![]() 服務(wù)機(jī)構(gòu)評(píng)價(jià)的“滿意度指數(shù)”比對(duì)
服務(wù)機(jī)構(gòu)評(píng)價(jià)的“滿意度指數(shù)”比對(duì)![]() 服務(wù)機(jī)構(gòu)評(píng)價(jià)的“滿意度指數(shù)”高的概率為 0.3 .
服務(wù)機(jī)構(gòu)評(píng)價(jià)的“滿意度指數(shù)”高的概率為 0.3 .
(3)如果從學(xué)生對(duì)![]() 兩服務(wù)機(jī)構(gòu)評(píng)價(jià)的“滿意度指數(shù)”的期望角度看:
兩服務(wù)機(jī)構(gòu)評(píng)價(jià)的“滿意度指數(shù)”的期望角度看:
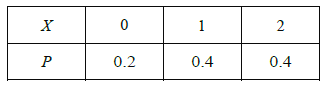
![]() 服務(wù)機(jī)構(gòu)“滿意度指數(shù)”
服務(wù)機(jī)構(gòu)“滿意度指數(shù)”![]() 的分布列為:
的分布列為:
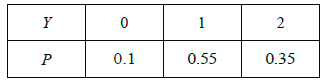
![]() 服務(wù)機(jī)構(gòu)“滿意度指數(shù)”
服務(wù)機(jī)構(gòu)“滿意度指數(shù)”![]() 的分布列為:
的分布列為:
因?yàn)?/span>![]() ;
;
![]() ,
,
所以![]() ,會(huì)選擇
,會(huì)選擇![]() 服務(wù)機(jī)構(gòu).
服務(wù)機(jī)構(gòu).


 名校通行證有效作業(yè)系列答案
名校通行證有效作業(yè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
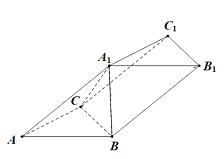
【題目】若圖,在三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,且
,且![]() 和
和![]() 均為正三角形.
均為正三角形.
(1)在![]() 上找一點(diǎn)
上找一點(diǎn)![]() ,使得
,使得![]() 平面
平面![]() ,并說(shuō)明理由.
,并說(shuō)明理由.
(2)若![]() 的面積為
的面積為![]() ,求四棱錐
,求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】【2018屆山西省太原十二中高三上學(xué)期1月月考】運(yùn)動(dòng)員甲在最近![]() 場(chǎng)
場(chǎng)![]() 比賽中所得分?jǐn)?shù)的莖葉圖如圖所示,由于疏忽,莖葉圖中的兩個(gè)數(shù)據(jù)上出行了污漬,導(dǎo)致這兩個(gè)數(shù)字無(wú)法辨認(rèn),但統(tǒng)計(jì)員記得除掉污漬
比賽中所得分?jǐn)?shù)的莖葉圖如圖所示,由于疏忽,莖葉圖中的兩個(gè)數(shù)據(jù)上出行了污漬,導(dǎo)致這兩個(gè)數(shù)字無(wú)法辨認(rèn),但統(tǒng)計(jì)員記得除掉污漬![]() 處的數(shù)字不影響整體中位數(shù),且這六個(gè)數(shù)據(jù)的平均值為
處的數(shù)字不影響整體中位數(shù),且這六個(gè)數(shù)據(jù)的平均值為![]() .
.
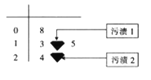
(1)求污漬![]() 處的數(shù)字;
處的數(shù)字;
(2)籃球運(yùn)動(dòng)員乙在最近![]() 場(chǎng)
場(chǎng)![]() 的比賽中所得分?jǐn)?shù)為
的比賽中所得分?jǐn)?shù)為![]() .試分別以各自
.試分別以各自![]() 場(chǎng)比賽得分的平均數(shù)與方差來(lái)分析這兩名籃球運(yùn)動(dòng)員的發(fā)揮水平.
場(chǎng)比賽得分的平均數(shù)與方差來(lái)分析這兩名籃球運(yùn)動(dòng)員的發(fā)揮水平.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某花店每天以每枝5元的價(jià)格從農(nóng)場(chǎng)購(gòu)進(jìn)若干枝玫瑰花,然后以每枝10元的價(jià)格出售.如果當(dāng)天賣不完,剩下的玫瑰花作垃圾處理.
(1)若花店一天購(gòu)進(jìn)17枝玫瑰花,求當(dāng)天的利潤(rùn)y(單位:元)關(guān)于當(dāng)天需求量n(單位:枝,n∈N)的函數(shù)解析式;
(2)花店記錄了100天玫瑰花的日需求量(單位:枝),整理得下表:
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
頻數(shù) | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①假設(shè)花店在這100天內(nèi)每天購(gòu)進(jìn)17枝玫瑰花,求這100天的日利潤(rùn)(單位:元)的平均數(shù);
②若花店一天購(gòu)進(jìn)17枝玫瑰花,以100天記錄的各需求量的頻率作為各需求量發(fā)生的概率,求當(dāng)天的利潤(rùn)不少于75元的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在三棱柱![]() 中,底面
中,底面![]() 是邊長(zhǎng)為2的等邊三角形,平面
是邊長(zhǎng)為2的等邊三角形,平面![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,且
,且![]() 平面
平面![]() .
.

(1)求證: ![]() ;
;
(2)若四邊形![]() 是正方形,且
是正方形,且![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1,梯形![]() 中,
中, ![]() 為
為![]() 中點(diǎn).將
中點(diǎn).將![]() 沿
沿![]() 翻折到
翻折到![]() 的位置,如圖2.
的位置,如圖2.

(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)設(shè)![]() 分別為
分別為![]() 和
和![]() 的中點(diǎn),試比較三棱錐
的中點(diǎn),試比較三棱錐![]() 和三棱錐
和三棱錐![]() (圖中未畫出)的體積大小,并說(shuō)明理由.
(圖中未畫出)的體積大小,并說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】選修4-5:不等式選講
已知函數(shù)![]()
(Ⅰ)求不等式![]() 的解集;
的解集;
(Ⅱ)已知函數(shù)![]() 的最小值為
的最小值為![]() ,若實(shí)數(shù)
,若實(shí)數(shù)![]() 且
且![]() ,求
,求![]() 的
的
最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() :
: ![]() 過(guò)點(diǎn)
過(guò)點(diǎn)![]() ,
, ![]() ,
, ![]() 分別是橢圓的左、右焦點(diǎn),以原點(diǎn)為圓心,橢圓
分別是橢圓的左、右焦點(diǎn),以原點(diǎn)為圓心,橢圓![]() 的短軸長(zhǎng)為直徑的圓與直線
的短軸長(zhǎng)為直徑的圓與直線![]() 相切.
相切.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過(guò)點(diǎn)![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
, ![]() ,求
,求![]() 內(nèi)切圓面積的最大值和此時(shí)直線
內(nèi)切圓面積的最大值和此時(shí)直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,
, ![]() .
.
(1)當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 的圖象在
的圖象在![]() 處的切線方程;
處的切線方程;
(2)若函數(shù)![]() 在定義域上為單調(diào)增函數(shù).
在定義域上為單調(diào)增函數(shù).
①求![]() 最大整數(shù)值;
最大整數(shù)值;
②證明: ![]() .
.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com