
【題目】已知函數![]() 在
在![]() 單調遞增,其中
單調遞增,其中![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,當
,當![]() 時,試比較
時,試比較![]() 與
與![]() 的大小關系(其中
的大小關系(其中![]() 是
是![]() 的導函數),請寫出詳細的推理過程;
的導函數),請寫出詳細的推理過程;
(3)當![]() 時,
時, ![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)略 (3)
(2)略 (3)![]()
【解析】試題分析:函數在某區間上單調遞增,只需函數的導數大于零在此區間上恒成立,利用恒成立極值原理求出![]() 滿足的條件,求出
滿足的條件,求出![]() 的值;第二步比較大小可以轉化為研究函數
的值;第二步比較大小可以轉化為研究函數![]() 的單調性和極值問題去解決,第三步可以利用作差法構造函數,通過利用導數研究函數單調性和極值,達到證明不等式的目的.
的單調性和極值問題去解決,第三步可以利用作差法構造函數,通過利用導數研究函數單調性和極值,達到證明不等式的目的.
試題解析:
(1)∵![]() 在
在![]() 單調遞增,
單調遞增,
∴![]()
![]() 在
在![]() 上恒成立,即
上恒成立,即![]() (
(![]() )恒成立,
)恒成立,
∵當![]() 時,
時, ![]() ,
,
∴![]() ,又
,又![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() .
.
(2)由(1)可知![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
令![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() 在
在![]() 上單調遞增,∴
上單調遞增,∴![]() ,
,
令![]() ,則
,則![]() 在
在![]() 單調遞減,
單調遞減,
∵![]() ,
, ![]() ,
,
∴![]() ,使得
,使得![]() 在
在![]() 單調遞增,在
單調遞增,在![]() 單調遞減,
單調遞減,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
又兩個函數的最小值不同時取得,
∴![]() ,即
,即![]() .
.
(3)∵![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
令![]() ,則
,則![]() ,
,
由(1)得![]() ,即
,即![]() (
(![]() ),∴
),∴![]() (
(![]() ),
),
即![]() (
(![]() ),∴
),∴![]() ,
,
∴![]() ,
,
當![]() 時,∵
時,∵![]() ,∴
,∴![]() ,
,
∴![]() 單調遞減,∴
單調遞減,∴![]() ,符合題意;
,符合題意;
當![]() 時,
時, ![]() 在
在![]() 上單調遞增,
上單調遞增,
∴![]() ,
,
∴![]() 單調遞增,∴
單調遞增,∴![]() 符合題意,
符合題意,
當![]() 時,
時, ![]() ,∴
,∴![]() 在
在![]() 上單調遞增,
上單調遞增,
又![]() ,且
,且![]() ,
, ![]() ,
,
∴![]() 在
在![]() 存在唯一零點
存在唯一零點![]() ,
,
![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增,
單調遞增,
∴當![]() 時,
時, ![]() ,
,
∴![]() 在
在![]() 單調遞減,∴
單調遞減,∴![]() ,不合題意.
,不合題意.
綜上, ![]() .
.


 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:高中數學 來源: 題型:
【題目】已知不交于同一點的三條直線l1:4x+y﹣4=0,l2:mx+y=0,l3:x﹣my﹣4=0
(1)當這三條直線不能圍成三角形時,求實數m的值.
(2)當l3與l1 , l2都垂直時,求兩垂足間的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中點. 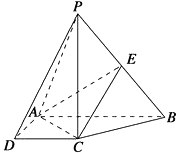
(1)求證:CE∥平面PAD;
(2)若二面角P﹣AC﹣E的余弦值為 ![]() ,求直線PA與平面EAC所成角的正弦值.
,求直線PA與平面EAC所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() +log2x.
+log2x.
(1)求f(2),f( ![]() ),f(4),f(
),f(4),f( ![]() )的值,并計算f(2)+f(
)的值,并計算f(2)+f( ![]() ),f(4)+f(
),f(4)+f( ![]() );
);
(2)求f(1)+f(2)+f(3)+…+f(2016)+f( ![]() )+f(
)+f( ![]() )+…f(
)+…f( ![]() )的值.
)的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數y=f(x)圖象上不同兩點A(x1 , y1),B(x2 , y2)處的切線的斜率分別是kA , kB , 規定φ(A,B)= ![]() 叫曲線y=f(x)在點A與點B之間的“彎曲度”,給出以下命題: 1)函數y=x3﹣x2+1圖象上兩點A、B的橫坐標分別為1,2,則φ(A,B)>
叫曲線y=f(x)在點A與點B之間的“彎曲度”,給出以下命題: 1)函數y=x3﹣x2+1圖象上兩點A、B的橫坐標分別為1,2,則φ(A,B)> ![]() ;
;
2)存在這樣的函數,圖象上任意兩點之間的“彎曲度”為常數;
3)設點A、B是拋物線,y=x2+1上不同的兩點,則φ(A,B)≤2;
4)設曲線y=ex上不同兩點A(x1 , y1),B(x2 , y2),且x1﹣x2=1,若tφ(A,B)<1恒成立,則實數t的取值范圍是(﹣∞,1);
以上正確命題的序號為(寫出所有正確的)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點![]() 是
是![]() 軸上的一個定點,其橫坐標為
軸上的一個定點,其橫坐標為![]() (
(![]() ),已知當
),已知當![]() 時,動圓
時,動圓![]() 過點
過點![]() 且與直線
且與直線![]() 相切,記動圓
相切,記動圓![]() 的圓心
的圓心![]() 的軌跡為
的軌跡為![]() .
.
(Ⅰ)求曲線![]() 的方程;
的方程;
(Ⅱ)當![]() 時,若直線
時,若直線![]() 與曲線
與曲線![]() 相切于點
相切于點![]() (
(![]() ),且
),且![]() 與以定點
與以定點![]() 為圓心的動圓
為圓心的動圓![]() 也相切,當動圓
也相切,當動圓![]() 的面積最小時,證明:
的面積最小時,證明: ![]() 、
、![]() 兩點的橫坐標之差為定值.
兩點的橫坐標之差為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列四個命題:
(1)函數f(x)在x>0時是增函數,x<0時也是增函數,所以f(x)是增函數;
(2)若m=loga2,n=logb2且m>n,則a<b;
(3)函數f(x)=x2+2(a﹣1)x+2在區間(﹣∞,4]上是減函數,則實數a的取值范圍是a≤﹣3;
(4)y=log ![]() (x2+x﹣2)的減區間為(1,+∞).
(x2+x﹣2)的減區間為(1,+∞).
其中正確的個數是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com