
【題目】已知數(shù)列![]() 的前
的前![]() 項和
項和![]() 滿足
滿足![]() (
(![]() ,
,![]() 為常數(shù),
為常數(shù),![]() ,且
,且![]() ),
),![]() ,
,![]() ,若存在正整數(shù)
,若存在正整數(shù)![]() ,使得
,使得![]() 成立;數(shù)列
成立;數(shù)列![]() 是首項為2,公差為
是首項為2,公差為![]() 的等差數(shù)列,
的等差數(shù)列,![]() 為其前
為其前![]() 項和,則以下結(jié)論正確的是( )
項和,則以下結(jié)論正確的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】B
【解析】
根據(jù)![]() ,
,![]() ,
,![]() ,令
,令![]() ,得到
,得到![]() ,進而得到
,進而得到![]() ,由
,由![]() ,
,![]() ,轉(zhuǎn)化為
,轉(zhuǎn)化為![]() ,
,![]() ,再根據(jù)
,再根據(jù)![]() ,
,![]() ,得到這個數(shù)列的奇數(shù)項恒負(fù)且遞增,偶數(shù)項恒正且遞減,則存在正整數(shù)
,得到這個數(shù)列的奇數(shù)項恒負(fù)且遞增,偶數(shù)項恒正且遞減,則存在正整數(shù)![]() ,使得
,使得![]() 成立,轉(zhuǎn)化為存在正整數(shù)
成立,轉(zhuǎn)化為存在正整數(shù)![]() ,有
,有![]() 成立,得到d的范圍,再利用數(shù)列
成立,得到d的范圍,再利用數(shù)列![]() 是首項為2,公差為
是首項為2,公差為![]() 的等差數(shù)列求解.
的等差數(shù)列求解.
因為![]() ,
,![]() ,
,![]() ,
,
所以![]() ,解得
,解得![]() ,
,
所以![]() .
.
因為![]() ,
,![]() ,
,
故![]() ,
,![]() (即奇數(shù)項為負(fù),偶數(shù)項為正),
(即奇數(shù)項為負(fù),偶數(shù)項為正),
又因為![]() ,
,![]() ,
,
所以這個數(shù)列的奇數(shù)項恒負(fù)且遞增,偶數(shù)項恒正且遞減,
所以條件轉(zhuǎn)化為存在正整數(shù)![]() ,使得
,使得![]() ,
,
只需![]() ,即
,即![]() .
.
因為![]() ,
,![]() ,所以
,所以![]() ,所以A項不正確,B項正確;
,所以A項不正確,B項正確;
因為![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() 與
與![]() 的大小無法判斷.
的大小無法判斷.
故選:B


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市在開展創(chuàng)建“全國文明城市”活動中,工作有序扎實,成效顯著,尤其是城市環(huán)境衛(wèi)生大為改觀,深得市民好評.“創(chuàng)文”過程中,某網(wǎng)站推出了關(guān)于環(huán)境治理和保護問題情況的問卷調(diào)查,現(xiàn)從參與問卷調(diào)查的人群中隨機選出200人,并將這200人按年齡分組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示.
,得到的頻率分布直方圖如圖所示.
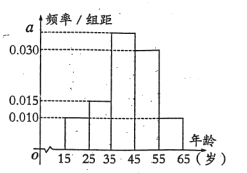
(1)求出a的值;
(2)若已從年齡較小的第1,2組中用分層抽樣的方法抽取5人,現(xiàn)要再從這5人中隨機抽取3人進行問卷調(diào)查,設(shè)第2組抽到![]() 人,求隨機變量
人,求隨機變量![]() 的分布列及數(shù)學(xué)期望
的分布列及數(shù)學(xué)期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某班同學(xué)在假期進行社會實踐活動,對![]() 歲的人群隨機抽取n人進行了一次當(dāng)前投資生活方式——“房地產(chǎn)投資”的調(diào)查,得到如下統(tǒng)計和各年齡段人數(shù)頻率分布直方圖:
歲的人群隨機抽取n人進行了一次當(dāng)前投資生活方式——“房地產(chǎn)投資”的調(diào)查,得到如下統(tǒng)計和各年齡段人數(shù)頻率分布直方圖:
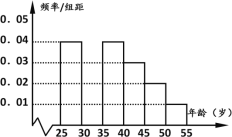
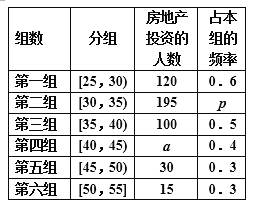
(Ⅰ)求![]() ,
,![]() ,
,![]() 的值;
的值;
(Ⅱ)從年齡在![]() 歲的“房地產(chǎn)投資”人群中采取分層抽樣法抽取9人參加投資管理學(xué)習(xí)活動,其中選取3人作為代表發(fā)言,記選取的3名代表中年齡在
歲的“房地產(chǎn)投資”人群中采取分層抽樣法抽取9人參加投資管理學(xué)習(xí)活動,其中選取3人作為代表發(fā)言,記選取的3名代表中年齡在![]() 歲的人數(shù)為
歲的人數(shù)為![]() ,求
,求![]() 的分布列和期望
的分布列和期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() ,平面
,平面![]() 平面PAD,E是
平面PAD,E是![]() 的中點,F是DC上一點,G是PC上一點,且
的中點,F是DC上一點,G是PC上一點,且![]() ,
,![]() .
.
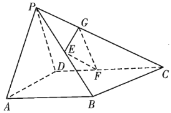
(1)求證:平面![]() 平面PAB;
平面PAB;
(2)若![]() ,
,![]() ,求直線PB與平面ABCD所成角的正弦值.
,求直線PB與平面ABCD所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,若
,若![]() 的圖象上相鄰兩條對稱軸的距離為
的圖象上相鄰兩條對稱軸的距離為![]() ,圖象過點
,圖象過點![]() .
.
(1)求![]() 的表達式和
的表達式和![]() 的遞增區(qū)間;
的遞增區(qū)間;
(2)將函數(shù)![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度,再將圖象上各點的橫坐標(biāo)伸長到原來的2倍(縱坐標(biāo)不變),得到函數(shù)
個單位長度,再將圖象上各點的橫坐標(biāo)伸長到原來的2倍(縱坐標(biāo)不變),得到函數(shù)![]() 的圖象.若函數(shù)
的圖象.若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上有且只有一個零點,求實數(shù)
上有且只有一個零點,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知三棱錐![]() 的四個頂點都在球
的四個頂點都在球![]() 的表面上,
的表面上,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,則球
,則球![]() 的半徑為______;若
的半徑為______;若![]() 是
是![]() 的中點,過點
的中點,過點![]() 作球
作球![]() 的截面,則截面面積的最小值是______.
的截面,則截面面積的最小值是______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某項針對我國《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)》的研究中,列出各個學(xué)段每個主題所包含的條目數(shù)(如下表),下圖是統(tǒng)計表的條目數(shù)轉(zhuǎn)化為百分比,按各學(xué)段繪制的等高條形圖,由圖表分析得出以下四個結(jié)論,其中錯誤的是( )
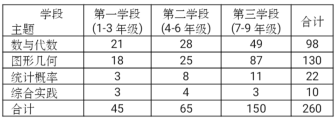
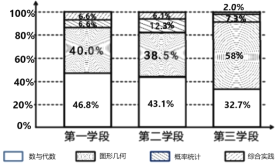
A.除了“綜合實踐”外,其它三個領(lǐng)域的條目數(shù)都隨著學(xué)段的升高而增加,尤其“圖象幾何” 在第三學(xué)段增加較多,約是第二學(xué)段的![]() 倍.
倍.
B.所有主題中,三個學(xué)段的總和“圖形幾何”條目數(shù)最多,占50%,綜合實踐最少,約占4% .
C.第一、二學(xué)段“數(shù)與代數(shù)”條目數(shù)最多,第三學(xué)段“圖形幾何”條目數(shù)最多.
D.“數(shù)與代數(shù)”條目數(shù)雖然隨著學(xué)段的增長而增長,而其百分比卻一直在減少.“圖形幾何”條目數(shù),百分比都隨學(xué)段的增長而增長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,已知直線![]() 的參數(shù)方程為
的參數(shù)方程為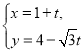 (
(![]() 是參數(shù)),以原點為極點,
是參數(shù)),以原點為極點,![]() 軸的非負(fù)半軸
軸的非負(fù)半軸
為極軸,建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(Ⅰ)求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(Ⅱ)設(shè)點![]() 在曲線
在曲線![]() 上,曲線
上,曲線![]() 在點
在點![]() 處的切線與直線
處的切線與直線![]() 垂直,求點
垂直,求點![]() 的直角坐標(biāo).
的直角坐標(biāo).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com