
【題目】函數(shù)f(x)=Asin(x+φ)(A>0,0<<4,|φ|< ![]() )過點(0,
)過點(0, ![]() ),且當x=
),且當x= ![]() 時,函數(shù)f(x)取得最大值1.
時,函數(shù)f(x)取得最大值1.
(1)將函數(shù)f(x)的圖象向右平移 ![]() 個單位得到函數(shù)g(x),求函數(shù)g(x)的表達式;
個單位得到函數(shù)g(x),求函數(shù)g(x)的表達式;
(2)在(1)的條件下,函數(shù)h(x)=f(x)+g(x)+2cos2x﹣1,如果對于x1 , x2∈R,都有h(x1)≤h(x)≤h(x2),求|x1﹣x2|的最小值.
【答案】
(1)解:由題意A=1,將點(0, ![]() )代入解得
)代入解得 ![]() ,
, ![]() ,
,
再根據(jù) ![]() ,結(jié)合0<<4,
,結(jié)合0<<4,
所以=2, ![]() .
.
將函數(shù)f(x)的圖象向右平移 ![]() 個單位得到函數(shù)
個單位得到函數(shù) ![]() 的圖象
的圖象
(2)解:函數(shù)h(x)=f(x)+g(x)+2cos2x﹣1=2sin(2x+ ![]() ),故函數(shù)的周期T=π.
),故函數(shù)的周期T=π.
對于x1,x2∈R,都有h(x1)≤h(x)≤h(x2),故|x1﹣x2|的最小值為 ![]()
【解析】(1)由函數(shù)的最值求出A,由特殊點的坐標求出φ的值,由五點法作圖求出ω,可得f(x)的解析式,再根據(jù)y=Asin(ωx+φ)的圖象變換規(guī)律,求得g(x)的解析式.(2)由條件利用正弦函數(shù)的最值以及周期性,求得|x1﹣x2|的最小值.
【考點精析】掌握函數(shù)y=Asin(ωx+φ)的圖象變換是解答本題的根本,需要知道圖象上所有點向左(右)平移![]() 個單位長度,得到函數(shù)
個單位長度,得到函數(shù)![]() 的圖象;再將函數(shù)
的圖象;再將函數(shù)![]() 的圖象上所有點的橫坐標伸長(縮短)到原來的
的圖象上所有點的橫坐標伸長(縮短)到原來的![]() 倍(縱坐標不變),得到函數(shù)
倍(縱坐標不變),得到函數(shù)![]() 的圖象;再將函數(shù)
的圖象;再將函數(shù)![]() 的圖象上所有點的縱坐標伸長(縮短)到原來的
的圖象上所有點的縱坐標伸長(縮短)到原來的![]() 倍(橫坐標不變),得到函數(shù)
倍(橫坐標不變),得到函數(shù)![]() 的圖象.
的圖象.


 暑假作業(yè)暑假快樂練西安出版社系列答案
暑假作業(yè)暑假快樂練西安出版社系列答案 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業(yè)鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業(yè)鄭州大學出版社系列答案科目:高中數(shù)學 來源: 題型:
【題目】隨著手機的發(fā)展,“微信”越來越成為人們交流的一種方式.某機構(gòu)對“使用微信交流”的態(tài)度進行調(diào)查,隨機抽取了50人,他們年齡的頻數(shù)分布及對“使用微信交流”贊成人數(shù)如下表.
年齡(單位:歲) |
|
|
|
|
|
|
頻數(shù) | 5 | 10 | 15 | 10 | 5 | 5 |
贊成人數(shù) | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年齡”45歲為分界點,由以上統(tǒng)計數(shù)據(jù)完成下面 ![]() 列聯(lián)表,并判斷是否有99%的把握認為“使用微信交流”的態(tài)度與人的年齡有關(guān);
列聯(lián)表,并判斷是否有99%的把握認為“使用微信交流”的態(tài)度與人的年齡有關(guān);
年齡不低于45歲的人數(shù) | 年齡低于45歲的人數(shù) | 合計 | |
贊成 | |||
不贊成 | |||
合計 |
(Ⅱ)若從年齡在 ![]() 和
和 ![]() 的被調(diào)查人中按照分層抽樣的方法選取6人進行追蹤調(diào)查,并給予其中3人“紅包”獎勵,求3人中至少有1人年齡在
的被調(diào)查人中按照分層抽樣的方法選取6人進行追蹤調(diào)查,并給予其中3人“紅包”獎勵,求3人中至少有1人年齡在 ![]() 的概率.
的概率.
參考數(shù)據(jù)如下:
附臨界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 的觀測值:
的觀測值: ![]() (其中
(其中 ![]() )
)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓 ![]() 的半焦距為
的半焦距為 ![]() ,原點
,原點 ![]() 到經(jīng)過兩點
到經(jīng)過兩點 ![]() 的直線的距離為
的直線的距離為 ![]() .
.
(Ⅰ)求橢圓 ![]() 的離心率;
的離心率;
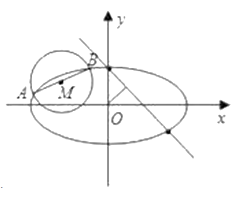
(Ⅱ)如圖, ![]() 是圓
是圓 ![]() 的一條直徑,若橢圓
的一條直徑,若橢圓 ![]() 經(jīng)過
經(jīng)過 ![]() 兩點,求橢圓
兩點,求橢圓 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若定義域為R的奇函數(shù)f(x)滿足f(1+x)=﹣f(x),則下列結(jié)論: ①f(x)的圖象關(guān)于點 ![]() 對稱;
對稱;
②f(x)的圖象關(guān)于直線 ![]() 對稱;
對稱;
③f(x)是周期函數(shù),且2個它的一個周期;
④f(x)在區(qū)間(﹣1,1)上是單調(diào)函數(shù).
其中正確結(jié)論的序號是 . (填上你認為所有正確結(jié)論的序號)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)判斷并證明函數(shù)![]() 的奇偶性;
的奇偶性;
(2)判斷當![]() 時函數(shù)
時函數(shù)![]() 的單調(diào)性,并用定義證明;
的單調(diào)性,并用定義證明;
(3)若![]() 定義域為
定義域為![]() ,解不等式
,解不等式![]() .
.
【答案】(1)奇函數(shù)(2)增函數(shù)(3)![]()
【解析】試題分析:(1)判斷與證明函數(shù)的奇偶性,首先要確定函數(shù)的定義域是否關(guān)于原點對稱,再判斷f(-x)與f(x)的關(guān)系,如果對定義域上的任意x,都滿足f(-x)=f(x)就是偶函數(shù),如果f(-x)=-f(x)就是奇函數(shù),否則是非奇非偶函數(shù)。(2)利函數(shù)單調(diào)性定義證明單調(diào)性,按假設,作差,化簡,判斷,下結(jié)論五個步驟。(3)由(1)(2)奇函數(shù)![]() 在(-1,1)為單調(diào)函數(shù),
在(-1,1)為單調(diào)函數(shù),
原不等式變形為f(2x-1)<-f(x),即f(2x-1)<f(-x),再由函數(shù)的單調(diào)性及定義(-1,1)求解得x范圍。
試題解析:(1)函數(shù)![]() 為奇函數(shù).證明如下:
為奇函數(shù).證明如下:
![]() 定義域為
定義域為![]()
又![]()
![]() 為奇函數(shù)
為奇函數(shù)
(2)函數(shù)![]() 在(-1,1)為單調(diào)函數(shù).證明如下:
在(-1,1)為單調(diào)函數(shù).證明如下:
任取![]() ,則
,則
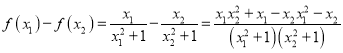
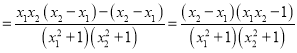
![]()
![]() ,
, ![]()
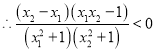
即![]()
故![]() 在(-1,1)上為增函數(shù)
在(-1,1)上為增函數(shù)
(3)由(1)、(2)可得
![]() 則
則
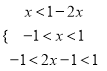 解得:
解得: ![]()
所以,原不等式的解集為![]()
【點睛】
(1)奇偶性:判斷與證明函數(shù)的奇偶性,首先要確定函數(shù)的定義域是否關(guān)于原點對稱,再判斷f(-x)與f(x)的關(guān)系,如果對定義域上的任意x,都滿足f(-x)=f(x)就是偶函數(shù),如果f(-x)=-f(x)就是奇函數(shù),否則是非奇非偶函數(shù)。
(2)單調(diào)性:利函數(shù)單調(diào)性定義證明單調(diào)性,按假設,作差,化簡,定號,下結(jié)論五個步驟。
【題型】解答題
【結(jié)束】
22
【題目】已知函數(shù)![]() .
.
(1)若![]() 的定義域和值域均是
的定義域和值域均是![]() ,求實數(shù)
,求實數(shù)![]() 的值;
的值;
(2)若![]() 在區(qū)間
在區(qū)間![]() 上是減函數(shù),且對任意的
上是減函數(shù),且對任意的![]() ,都有
,都有![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若![]() ,且對任意的
,且對任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知在銳角△ABC中,a,b,c為角A,B,C所對的邊,且(b﹣2c)cosA=a﹣2acos2 ![]() .
.
(1)求角A的值;
(2)若a= ![]() ,則求b+c的取值范圍.
,則求b+c的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知定義在實數(shù)集R上的奇函數(shù)f(x)有最小正周期2,且當x∈(0,1)時, ![]() .
.
(Ⅰ)求函數(shù)f(x)在(-1,1)上的解析式;
(Ⅱ)判斷f(x)在(0,1)上的單調(diào)性;
(Ⅲ)當λ取何值時,方程f(x)=λ在(-1,1)上有實數(shù)解?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在正四面體P﹣ABC中,點M是棱PC的中點,點N是線段AB上一動點,且 ![]() ,設異面直線 NM 與 AC 所成角為α,當
,設異面直線 NM 與 AC 所成角為α,當 ![]() 時,則cosα的取值范圍是 .
時,則cosα的取值范圍是 .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
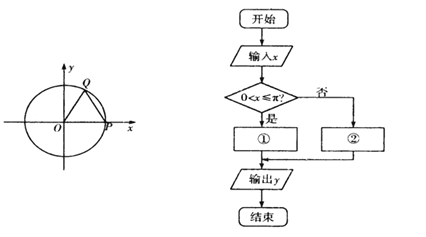
【題目】如圖,已知單位圓x2+y2=1與x軸正半軸交于點P,當圓上一動點Q從P出發(fā)沿逆時針方向旋轉(zhuǎn)一周回到P點后停止運動設OQ掃過的扇形對應的圓心角為xrad,當0<x<2π時,設圓心O到直線PQ的距離為y,y與x的函數(shù)關(guān)系式y(tǒng)=f(x)是如圖所示的程序框圖中的①②兩個關(guān)系式
(Ⅰ)寫出程序框圖中①②處的函數(shù)關(guān)系式;
(Ⅱ)若輸出的y值為2,求點Q的坐標.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com