
【題目】隨著手機的發展,“微信”越來越成為人們交流的一種方式.某機構對“使用微信交流”的態度進行調查,隨機抽取了50人,他們年齡的頻數分布及對“使用微信交流”贊成人數如下表.
年齡(單位:歲) |
|
|
|
|
|
|
頻數 | 5 | 10 | 15 | 10 | 5 | 5 |
贊成人數 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年齡”45歲為分界點,由以上統計數據完成下面 ![]() 列聯表,并判斷是否有99%的把握認為“使用微信交流”的態度與人的年齡有關;
列聯表,并判斷是否有99%的把握認為“使用微信交流”的態度與人的年齡有關;
年齡不低于45歲的人數 | 年齡低于45歲的人數 | 合計 | |
贊成 | |||
不贊成 | |||
合計 |
(Ⅱ)若從年齡在 ![]() 和
和 ![]() 的被調查人中按照分層抽樣的方法選取6人進行追蹤調查,并給予其中3人“紅包”獎勵,求3人中至少有1人年齡在
的被調查人中按照分層抽樣的方法選取6人進行追蹤調查,并給予其中3人“紅包”獎勵,求3人中至少有1人年齡在 ![]() 的概率.
的概率.
參考數據如下:
附臨界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 的觀測值:
的觀測值: ![]() (其中
(其中 ![]() )
)
【答案】解:(Ⅰ)根據條件得 ![]() 列聯表:
列聯表:
年齡不低于45歲的人數 | 年齡低于45歲的人數 | 合計 | |
贊成 | 10 | 27 | 37 |
不贊成 | 10 | 3 | 13 |
合 計 | 20 | 30 | 50 |
根據列聯表所給的數據代入公式得到: ![]()
所以有99%的把握認為“使用微信交流”的態度與人的年齡有關;
(Ⅱ)解:按照分層抽樣方法可知: ![]() 抽取:
抽取: ![]() (人);
(人);
![]() 抽取:
抽取: ![]() (人)
(人)
在上述抽取的6人中,年齡在 ![]() 有2人,年齡
有2人,年齡 ![]() 有4人.
有4人.
年齡在 ![]() 記為
記為 ![]() ;年齡在
;年齡在 ![]() 記為
記為 ![]() ,則從6人中任取3名的所有情況為:
,則從6人中任取3名的所有情況為: ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 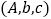 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 共20種情況,
共20種情況,
其中至少有一人年齡在 ![]() 歲情況有:
歲情況有: ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() ,共16種情況.
,共16種情況.
記至少有一人年齡在 ![]() 歲為事件
歲為事件 ![]() ,則
,則 ![]()
∴至少有一人年齡在 ![]() 歲之間的概率為
歲之間的概率為 ![]()
【解析】(1)由圖表可知求出樣本方差的值進行對比得出結論。(2)利用分層抽樣得出在每個年齡階段的人數為6人,根據題意列舉出從6人中任取三人的情況有20種,結合同意可得至少有一人在 [ 55 , 65 )的情況有16種,利用概率的定義求出其值即可。
【考點精析】解答此題的關鍵在于理解分層抽樣的相關知識,掌握先將總體中的所有單位按照某種特征或標志(性別、年齡等)劃分成若干類型或層次,然后再在各個類型或層次中采用簡單隨機抽樣或系用抽樣的辦法抽取一個子樣本,最后,將這些子樣本合起來構成總體的樣本.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2 ![]() sin(
sin( ![]() ωx)cos(
ωx)cos( ![]() ωx)+2cos2(
ωx)+2cos2( ![]() ωx)(ω>0),且函數f(x)的最小正周期為π.
ωx)(ω>0),且函數f(x)的最小正周期為π.
(1)求ω的值;
(2)求f(x)在區間 ![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD為梯形,CD∥AB,AB=2CD,AC交BD于O,銳角△PAD所在平面⊥底面ABCD,PA⊥BD,點Q在側棱PC上,且PQ=2QC.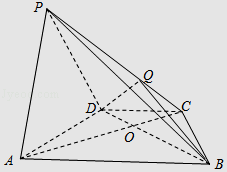
(1)求證:PA∥平面QBD;
(2)求證BD⊥AD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知△ABC三個頂點坐標為A(7,8),B(10,4),C(2,-4).
(1)求BC邊上的中線所在直線的方程;
(2)求BC邊上的高所在直線的方程.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】試題分析:(1)根據中點坐標公式求出![]() 中點
中點![]() 的坐標,根據斜率公式可求得
的坐標,根據斜率公式可求得![]() 的斜率,利用點斜式可求
的斜率,利用點斜式可求![]() 邊上的中線所在直線的方程;(2)先根據斜率公式求出
邊上的中線所在直線的方程;(2)先根據斜率公式求出![]() 的斜率,從而求出
的斜率,從而求出![]() 邊上的高所在直線的斜率為
邊上的高所在直線的斜率為![]() ,利用點斜式可求
,利用點斜式可求![]() 邊上的高所在直線的方程.
邊上的高所在直線的方程.
試題解析:(1)由B(10,4),C(2,-4),得BC中點D的坐標為(6,0),
所以AD的斜率為k=![]() =8,
=8,
所以BC邊上的中線AD所在直線的方程為y-0=8(x-6),
即8x-y-48=0.
(2)由B(10,4),C(2,-4),得BC所在直線的斜率為k=![]() =1,
=1,
所以BC邊上的高所在直線的斜率為-1,
所以BC邊上的高所在直線的方程為y-8=-(x-7),即x+y-15=0.
【題型】解答題
【結束】
17
【題目】已知直線l:x-2y+2m-2=0.
(1)求過點(2,3)且與直線l垂直的直線的方程;
(2)若直線l與兩坐標軸所圍成的三角形的面積大于4,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知點P(0,1)在圓C:x2+y2+2mx﹣2y+m2﹣4m+1=0內,若存在過點P的直線交圓C于A、B兩點,且△PBC的面積是△PAC的面積的2倍,則實數m的取值范圍為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列 ![]() 的前
的前 ![]() 項和為
項和為 ![]() ,且滿足
,且滿足 ![]() ,求數列
,求數列 ![]() 的通項公式.勤于思考的小紅設計了下面兩種解題思路,請你選擇其中一種并將其補充完整.
的通項公式.勤于思考的小紅設計了下面兩種解題思路,請你選擇其中一種并將其補充完整.
思路1:先設 ![]() 的值為1,根據已知條件,計算出
的值為1,根據已知條件,計算出 ![]() ,
, ![]() ,
, ![]() .
.
猜想: ![]() .
.
然后用數學歸納法證明.證明過程如下:
①當 ![]() 時, , 猜想成立
時, , 猜想成立
②假設 ![]() (
( ![]() N*)時,猜想成立,即
N*)時,猜想成立,即 ![]() .
.
那么,當 ![]() 時,由已知
時,由已知 ![]() ,得
,得 ![]() .
.
又 ![]() ,兩式相減并化簡,得
,兩式相減并化簡,得 ![]() (用含
(用含 ![]() 的代數式表示).
的代數式表示).
所以,當 ![]() 時,猜想也成立.
時,猜想也成立.
根據①和②,可知猜想對任何 ![]() N*都成立.
N*都成立.
思路2:先設 ![]() 的值為1,根據已知條件,計算出
的值為1,根據已知條件,計算出 ![]() .
.
由已知 ![]() ,寫出
,寫出 ![]() 與
與 ![]() 的關系式:
的關系式: ![]() ,
,
兩式相減,得 ![]() 與
與 ![]() 的遞推關系式:
的遞推關系式: ![]() .
.
整理: ![]() .
.
發現:數列 ![]() 是首項為 , 公比為的等比數列.
是首項為 , 公比為的等比數列.
得出:數列 ![]() 的通項公式
的通項公式 ![]() , 進而得到
, 進而得到 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的一系列對應值如下表:
的一系列對應值如下表:

(1)根據表格提供的數據求出函數![]() 的一個解析式;
的一個解析式;
(2)根據(1)的結果,若函數![]() 的周期為
的周期為![]() ,當
,當![]() 時,方程
時,方程![]() 恰有兩個不同的解,求實數
恰有兩個不同的解,求實數![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從2017年1月18日開始,支付寶用戶可以通過“![]() 掃‘福’字”和“參與螞蟻森林”兩種方式獲得福卡(愛國福、富強福、和諧福、友善福,敬業福),除夕夜
掃‘福’字”和“參與螞蟻森林”兩種方式獲得福卡(愛國福、富強福、和諧福、友善福,敬業福),除夕夜![]() ,每一位提前集齊五福的用戶都將獲得一份現金紅包.某髙校一個社團在年后開學后隨機調査了80位該校在讀大學生,就除夕夜
,每一位提前集齊五福的用戶都將獲得一份現金紅包.某髙校一個社團在年后開學后隨機調査了80位該校在讀大學生,就除夕夜![]() 之前是否集齊五福進行了一次調查(若未參與集五福的活動,則也等同于未集齊五福),得到具體數據如下表:
之前是否集齊五福進行了一次調查(若未參與集五福的活動,則也等同于未集齊五福),得到具體數據如下表:
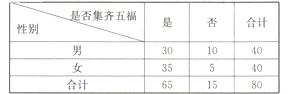
(1)計算這80位大學生集齊五福的頻率,并據此估算該校10000名在讀大學生中集齊五福的人數;
(2)為了解集齊五福的大學生明年是否愿意繼續參加集五福活動,該大學的學生會從集齊五福的學生中,選取2位男生和3位女生逐個進行采訪,最后再隨機選取3次采訪記錄放到該大學的官方網站上,求最后被選取的3次采訪對象中至少有一位男生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=Asin(x+φ)(A>0,0<<4,|φ|< ![]() )過點(0,
)過點(0, ![]() ),且當x=
),且當x= ![]() 時,函數f(x)取得最大值1.
時,函數f(x)取得最大值1.
(1)將函數f(x)的圖象向右平移 ![]() 個單位得到函數g(x),求函數g(x)的表達式;
個單位得到函數g(x),求函數g(x)的表達式;
(2)在(1)的條件下,函數h(x)=f(x)+g(x)+2cos2x﹣1,如果對于x1 , x2∈R,都有h(x1)≤h(x)≤h(x2),求|x1﹣x2|的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com