
【題目】如圖,四棱錐![]() 中,
中,![]() 平面ABCD,底面ABCD是正方形,
平面ABCD,底面ABCD是正方形,![]() ,E為PC上一點(diǎn),當(dāng)F為DC的中點(diǎn)時,EF平行于平面PAD.
,E為PC上一點(diǎn),當(dāng)F為DC的中點(diǎn)時,EF平行于平面PAD.
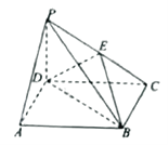
(Ⅰ)求證:![]() 平面PCB;
平面PCB;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)證明見解析;(Ⅱ)![]()
【解析】
(Ⅰ)![]() 平面
平面![]() 可得
可得![]() ,從而證出
,從而證出![]() 平面
平面![]() ,則
,則![]() ,
,
從而可證出![]() 平面
平面![]() ;
;
(Ⅱ)以點(diǎn)![]() 為坐標(biāo)原點(diǎn),分別以直線
為坐標(biāo)原點(diǎn),分別以直線![]() ,
,![]() ,
,![]() 為
為![]() 軸,
軸,![]() 軸,
軸,![]() 軸,建立空間直角坐標(biāo)系,求得各點(diǎn)的坐標(biāo),求出平面
軸,建立空間直角坐標(biāo)系,求得各點(diǎn)的坐標(biāo),求出平面![]() 和平面
和平面![]() 的的一個法向量,再根據(jù)法向量求出二面角.
的的一個法向量,再根據(jù)法向量求出二面角.
(Ⅰ)證:![]() 平面
平面![]() ,
,![]() ,
,
又![]() 正方形
正方形![]() 中,
中,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,![]() ,
,
![]() ,當(dāng)
,當(dāng)![]() 為
為![]() 的中點(diǎn)時,
的中點(diǎn)時,![]() 平行平面
平行平面![]() ,所以
,所以![]() 是
是![]() 的中點(diǎn),
的中點(diǎn),
![]() ,
,![]() ,
,![]() 平面
平面![]() ;
;
(Ⅱ)解:以點(diǎn)![]() 為坐標(biāo)原點(diǎn),分別以直線
為坐標(biāo)原點(diǎn),分別以直線![]() ,
,![]() ,
,![]() 為
為![]() 軸,
軸,![]() 軸,
軸,![]() 軸,建立如圖所示的空間直角坐標(biāo)系,
軸,建立如圖所示的空間直角坐標(biāo)系,

則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
設(shè)平面![]() 的法向量為
的法向量為![]() ,則
,則![]() ,
,![]() ,
,
![]() ,令
,令![]() ,得到
,得到![]() ,
,![]() ,
,![]() ;
;
又![]() ,
,![]() ,
,![]() ,且
,且![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 的一個法向量為
的一個法向量為![]() ;
;
設(shè)二面角![]() 的平面角為
的平面角為![]() ,由圖可知角
,由圖可知角![]() 為銳角,
為銳角,
則![]() ,
,
![]() 二面角
二面角![]() 的余弦值為
的余弦值為![]() .
.


 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于定義域?yàn)?/span>D的函數(shù)f(x),若存在區(qū)間[m,n]![]() D,同時滿足下列條件:①f(x)在[m,n]上是單調(diào)的;②當(dāng)定義域是[m,n]時,f(x)的值域也是[m,n],則稱[m,n]為該函數(shù)的“和諧區(qū)間”.下列函數(shù)存在“和諧區(qū)間”的有( )
D,同時滿足下列條件:①f(x)在[m,n]上是單調(diào)的;②當(dāng)定義域是[m,n]時,f(x)的值域也是[m,n],則稱[m,n]為該函數(shù)的“和諧區(qū)間”.下列函數(shù)存在“和諧區(qū)間”的有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)a,b,c為實(shí)數(shù),f(x)=(x+a)(x2+bx+c),g(x)=(ax+1)(cx2+bx+1).記集合S={x|f(x)=0,x∈R},T={x|g(x)=0,x∈R}.若{S},{T}分別為集合S,T 的元素個數(shù),則下列結(jié)論不可能的是( )
A.{S}=1且{T}=0B.{S}=1且{T}=1C.{S}=2且{T}=2D.{S}=2且{T}=3
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)點(diǎn)P,Q分別是曲線y=xe﹣x(e是自然對數(shù)的底數(shù))和直線y=x+3上的動點(diǎn),則P,Q兩點(diǎn)間距離的最小值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】假設(shè)關(guān)于某設(shè)備的使用年限x(年)和所支出的維修費(fèi)用y萬元有如下的統(tǒng)計資料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)畫出散點(diǎn)圖并判斷是否線性相關(guān);
(2)如果線性相關(guān),求線性回歸方程;
(3)估計使用年限為10年時,維修費(fèi)用是多少?
附注:①參考公式:回歸方程![]() 中斜率和截距的最小二乘估計分別為
中斜率和截距的最小二乘估計分別為 ;
;
②參考數(shù)據(jù):![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如果存在非零常數(shù)![]() ,對于函數(shù)
,對于函數(shù)![]() 定義域上的任意
定義域上的任意![]() ,都有
,都有![]() 成立,那么稱函數(shù)為“
成立,那么稱函數(shù)為“![]() 函數(shù)”.
函數(shù)”.
(Ⅰ)若![]() ,
,![]() ,試判斷函數(shù)
,試判斷函數(shù)![]() 和
和![]() 是否是“
是否是“![]() 函數(shù)”?若是,請證明:若不是,主說明理由:
函數(shù)”?若是,請證明:若不是,主說明理由:
(Ⅱ)求證:若![]() 是單調(diào)函數(shù),則它是“
是單調(diào)函數(shù),則它是“![]() 函數(shù)”;
函數(shù)”;
(Ⅲ)若函數(shù)![]() 是“
是“![]() 函數(shù)”,求實(shí)數(shù)
函數(shù)”,求實(shí)數(shù)![]() 滿足的條件.
滿足的條件.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某公司為了解廣告投入對銷售收益的影響,在若干地區(qū)各投入4萬元廣告費(fèi)用,并將各地的銷售收益繪制成頻率分布直方圖(如圖所示),由于工作人員操作失誤,橫軸的數(shù)據(jù)丟失,但可以確定橫軸是從0開始計數(shù)的.
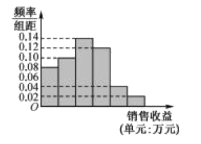
(1)根據(jù)頻率分布直方圖計算圖中各小長方形的寬度;
(2)試估計該公司在若干地區(qū)各投入4萬元廣告費(fèi)用之后,對應(yīng)銷售收益的平均值(以各組的區(qū)間中點(diǎn)值代表該組的取值);
(3)該公司按照類似的研究方法,測得另外一些數(shù)據(jù),并整理得到下表:
廣告投入 | 1 | 2 | 3 | 4 | 5 |
銷售收益 | 2 | 3 | 3 | 7 |
由表中的數(shù)據(jù)顯示,![]() 與
與![]() 之間存在著線性相關(guān)關(guān)系,請將(2)的結(jié)果填入空白欄,并求出
之間存在著線性相關(guān)關(guān)系,請將(2)的結(jié)果填入空白欄,并求出![]() 關(guān)于
關(guān)于![]() 的回歸直線方程.(參考公式:
的回歸直線方程.(參考公式: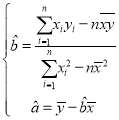 )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】![]() 年東京夏季奧運(yùn)會將設(shè)置
年東京夏季奧運(yùn)會將設(shè)置![]() 米男女混合泳接力這一新的比賽項(xiàng)目,比賽的規(guī)則是:每個參賽國家派出2男2女共計4名運(yùn)動員比賽,按照仰泳
米男女混合泳接力這一新的比賽項(xiàng)目,比賽的規(guī)則是:每個參賽國家派出2男2女共計4名運(yùn)動員比賽,按照仰泳![]() 蛙泳
蛙泳![]() 蝶泳
蝶泳![]() 自由泳的接力順序,每種泳姿
自由泳的接力順序,每種泳姿![]() 米且由一名運(yùn)動員完成, 每個運(yùn)動員都要出場. 現(xiàn)在中國隊(duì)確定了備戰(zhàn)該項(xiàng)目的4名運(yùn)動員名單,其中女運(yùn)動員甲只能承擔(dān)仰泳或者自由泳,男運(yùn)動員乙只能承擔(dān)蝶泳或自由泳,剩下的男女各一名運(yùn)動員則四種泳姿都可以上,那么中國隊(duì)共有( )種兵布陣的方式.
米且由一名運(yùn)動員完成, 每個運(yùn)動員都要出場. 現(xiàn)在中國隊(duì)確定了備戰(zhàn)該項(xiàng)目的4名運(yùn)動員名單,其中女運(yùn)動員甲只能承擔(dān)仰泳或者自由泳,男運(yùn)動員乙只能承擔(dān)蝶泳或自由泳,剩下的男女各一名運(yùn)動員則四種泳姿都可以上,那么中國隊(duì)共有( )種兵布陣的方式.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() :
:![]() 內(nèi)有一點(diǎn)
內(nèi)有一點(diǎn)![]() ,過
,過![]() 的兩條直線
的兩條直線![]() ,
,![]() 分別與拋物線
分別與拋物線![]() 交于
交于![]() ,
,![]() 和
和![]() ,
,![]() 兩點(diǎn),且滿足
兩點(diǎn),且滿足![]() ,
,![]() ,已知線段
,已知線段![]() 的中點(diǎn)為
的中點(diǎn)為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() .
.
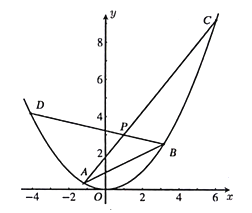
(1)求證:點(diǎn)![]() 的橫坐標(biāo)為定值;
的橫坐標(biāo)為定值;
(2)如果![]() ,點(diǎn)
,點(diǎn)![]() 的縱坐標(biāo)小于3,求
的縱坐標(biāo)小于3,求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com