
【題目】“綠水青山就是金山銀山”,為了保護環境,減少空氣污染,某空氣凈化器制造廠,決定投入生產某種惠民型的空氣凈化器.根據以往的生產銷售經驗得到年生產銷售的統計規律如下:①年固定生產成本為2萬元;②每生產該型號空氣凈化器1百臺,成本增加1萬元;③年生產x百臺的銷售收入 (萬元).假定生產的該型號空氣凈化器都能賣出(利潤=銷售收入﹣生產成本).
(萬元).假定生產的該型號空氣凈化器都能賣出(利潤=銷售收入﹣生產成本).
(1)為使該產品的生產不虧本,年產量x應控制在什么范圍內?
(2)該產品生產多少臺時,可使年利潤最大?
【答案】(1)100臺到550臺之間;(2)年產300臺時,可使利潤最大
【解析】
(1)由題意,成本函數為![]() ,從而年利潤函數為
,從而年利潤函數為![]() ,要使不虧本,利用分段函數和二次函數的性質,即可求解.
,要使不虧本,利用分段函數和二次函數的性質,即可求解.
(2)利用分段函數,求得每支上的最大值,即可得到函數的最大值,得到答案.
(1)由題意得,成本函數為![]() ,
,
從而年利潤函數為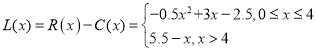 .
.
要使不虧本,只要L(x)≥0,
①當0≤x≤4時,由L(x)≥0得﹣0.5x2+3x﹣2.5≥0, 解得1≤x≤4,
②當x>4時,由L(x)≥0得5.5﹣x≥0, 解得4<x≤5.5
綜上1≤x≤5.5
答:若要該廠不虧本,產量x應控制在100臺到550臺之間
(2)當0≤x≤4時,L(x)= -0.5(x﹣3)2+2,
故當x =3時,L(x)max=2(萬元),
當x>4時,L(x)<1.5<2.
綜上,當年產300臺時,可使利潤最大


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知平面ADC∥平面A1B1C1 , B為線段AD的中點,△ABC≈△A1B1C1 , 四邊形ABB1A1為正方形,平面AA1C1C丄平面ADB1A1 , A1C1=A1A,∠C1A1A= ![]() ,M為棱A1C1的中點.
,M為棱A1C1的中點.
(Ⅰ)若N為線段DC1上的點,且直線MN∥平面ADB1A1 , 試確定點N的位置;
(Ⅱ)求平面MAD與平面CC1D所成的銳二面角的余弦值.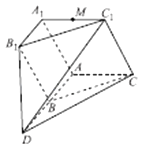
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)是定義在區間(0,+∞)內的單調函數,且對x∈(0,∞),都有f[f(x)﹣lnx]=e+1,設f′(x)為f(x)的導函數,則函數g(x)=f(x)﹣f′(x)的零點個數為( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某闖關游戲規則是:先后擲兩枚骰子,將此試驗重復n輪,第n輪的點數分別記為xn , yn , 如果點數滿足xn< ![]() ,則認為第n輪闖關成功,否則進行下一輪投擲,直到闖關成功,游戲結束.
,則認為第n輪闖關成功,否則進行下一輪投擲,直到闖關成功,游戲結束.
(Ⅰ)求第一輪闖關成功的概率;
(Ⅱ)如果第i輪闖關成功所獲的獎金數f(i)=10000× ![]() (單位:元),求某人闖關獲得獎金不超過1250元的概率;
(單位:元),求某人闖關獲得獎金不超過1250元的概率;
(Ⅲ)如果游戲只進行到第四輪,第四輪后不論游戲成功與否,都終止游戲,記進行的輪數為隨機變量X,求x的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() (a>b>0)的離心率為
(a>b>0)的離心率為 ![]() ,直線l:y=x+2與以原點為圓心、橢圓C的短半軸為半徑的圓O相切.
,直線l:y=x+2與以原點為圓心、橢圓C的短半軸為半徑的圓O相切.
(1)求橢圓C的方程;
(2)過橢圓C的左頂點A作直線m,與圓O相交于兩點R,S,若△ORS是鈍角三角形,求直線m的斜率k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,將一矩形花壇ABCD擴建成一個更大的矩形花壇AMPN,要求B點在AM上,D點在AN上,且對角線MN過點C,已知AB=2米,AD=1米.

(1)要使矩形AMPN的面積大于9平方米,則DN的長應在什么范圍內?
(2)當DN的長度為多少時,矩形花壇AMPN的面積最小?并求出最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com