
【題目】如圖,已知平面ADC∥平面A1B1C1 , B為線段AD的中點,△ABC≈△A1B1C1 , 四邊形ABB1A1為正方形,平面AA1C1C丄平面ADB1A1 , A1C1=A1A,∠C1A1A= ![]() ,M為棱A1C1的中點.
,M為棱A1C1的中點.
(Ⅰ)若N為線段DC1上的點,且直線MN∥平面ADB1A1 , 試確定點N的位置;
(Ⅱ)求平面MAD與平面CC1D所成的銳二面角的余弦值.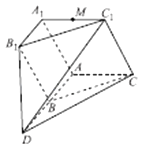
【答案】證明:(Ⅰ)連結A1D,直線MN∥平面ADB1A1 , MN平面A1C′1D, 平面A1C1D∩平面ADB1A1=A1D1 , ∴MN∥A1D,
又M為棱A1C1的中點,∴MN為△A1C1D的中位線,
∴N為DC1的中點.
(Ⅱ)設A1B1=1,則A1A=1,A1C1=1,因為B為AD的中點,所以AD=2,因為△ABC≌△A1B1C1 ,
所以A1C1=AC,又平面ABC∥平面A1B1C1 , 平面A1B1C1∩平面A1AOC1=A1C1 , 平面ABC∩平面A1AOC1=AO,
∴A1C1∥AC,所以四邊形A1ACC1是平行四邊形,又A1C1=A1A,所以A1ACC1是菱形,又∠C1A1A= ![]() ,
,
A1M= ![]() ,∴
,∴ ![]() ,∴AM⊥A1C1 , ∴AM⊥AC,∵AD⊥AA1 , 平面AA1C1C⊥平面ADB1A1 ,
,∴AM⊥A1C1 , ∴AM⊥AC,∵AD⊥AA1 , 平面AA1C1C⊥平面ADB1A1 ,
∴AD⊥平面AA1C1C,∴AD⊥AM,AD⊥AC,∴AM,AD,AC兩兩垂直,
以A為坐標原點,AD,AC,AM分別為x,y,z軸,
由題意可得:A(0,0,0),D(2,0,0),C(0,1,0),C1( ![]() ),∴
),∴ ![]() =(﹣2,1,0),
=(﹣2,1,0), 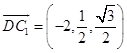 ,
,
設平面CC1D的法向量為: ![]() =(x,y,z),則
=(x,y,z),則 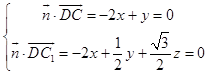 ,
,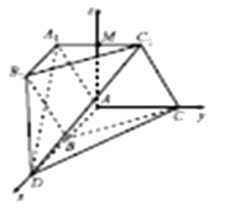
令z=2 ![]() ,可得y=6,x=3,可得
,可得y=6,x=3,可得 ![]() =(3,6,2
=(3,6,2 ![]() ),平面MAD的一個法向量為:
),平面MAD的一個法向量為: ![]() =(0,1,0),
=(0,1,0),
平面MAD與平面CC1D所成的銳二面角的余弦值為:cosθ=|cos ![]() |
|
=  =
= ![]() =
= ![]()
【解析】(Ⅰ)連結A1D,直線MN∥平面ADB1A1 , 推出MN∥A1D,說明MN為△A1C1D的中位線,得到N為DC1的中點.(Ⅱ)設A1B1=1,證明AD⊥AM,AD⊥AC,∴AM,AD,AC兩兩垂直,以A為坐標原點,AD,AC,AM分別為x,y,z軸,求出相關點的坐標,求出平面CC1D的法向量,平面MAD的一個法向量,利用空間向量的數量積求解即可.
【考點精析】認真審題,首先需要了解直線與平面平行的判定(平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行).


科目:高中數學 來源: 題型:
【題目】已知二次函數![]() 滿足
滿足![]() ,且
,且![]() 的最小值是
的最小值是![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若關于![]() 的方程
的方程![]() 在區間
在區間![]() 上有唯一實數根,求實數
上有唯一實數根,求實數![]() 的取值范圍;
的取值范圍;
(3)函數![]() ,對任意
,對任意![]() 都有
都有![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知t為實數,函數![]() ,其中
,其中![]()
(1)若![]() ,求
,求![]() 的取值范圍。
的取值范圍。
(2)當![]() 時,
時,![]() 的圖象始終在
的圖象始終在![]() 的圖象的下方,求t的取值范圍;
的圖象的下方,求t的取值范圍;
(3)設![]() ,當
,當![]() 時,函數
時,函數![]() 的值域為
的值域為![]() ,若
,若![]() 的最小值為
的最小值為![]() ,求實數a的值.
,求實數a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)是定義在區間(0,+∞)內的單調函數,且對x∈(0,∞),都有f[f(x)﹣lnx]=e+1,設f′(x)為f(x)的導函數,則函數g(x)=f(x)﹣f′(x)的零點個數為( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖甲所示,放在水平地面上的物體,受到方向不變的水平推力F的作用,F的大小與時間t的關系和物體運動速度v與時間t的關系如圖乙所示.下列判斷正確的是:
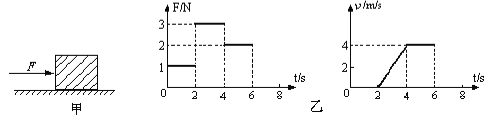
A.t=3s時,物體受到力的合力為零
B.t=6s時,將F撤掉,物體立刻靜止
C.2s~4s內物體所受摩擦力逐漸增大
D.t=1s時,物體所受摩擦力是1N
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“綠水青山就是金山銀山”,為了保護環境,減少空氣污染,某空氣凈化器制造廠,決定投入生產某種惠民型的空氣凈化器.根據以往的生產銷售經驗得到年生產銷售的統計規律如下:①年固定生產成本為2萬元;②每生產該型號空氣凈化器1百臺,成本增加1萬元;③年生產x百臺的銷售收入 (萬元).假定生產的該型號空氣凈化器都能賣出(利潤=銷售收入﹣生產成本).
(萬元).假定生產的該型號空氣凈化器都能賣出(利潤=銷售收入﹣生產成本).
(1)為使該產品的生產不虧本,年產量x應控制在什么范圍內?
(2)該產品生產多少臺時,可使年利潤最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com