
【題目】已知f(x)=lnx,g(x)= ![]() +mx+
+mx+ ![]() (m<0),直線l與函數f(x)的圖象相切,切點的橫坐標為1,且直線l與函數g(x)的圖象也相切.
(m<0),直線l與函數f(x)的圖象相切,切點的橫坐標為1,且直線l與函數g(x)的圖象也相切.
(1)求直線l的方程及實數m的值;
(2)若h(x)=f(x+1)﹣g′(x)(其中g′(x)是g(x)的導函數),求函數h(x)的最大值;
(3)當0<b<a時,求證:f(a+b)﹣f(2a)< ![]() .
.
【答案】
(1)解:∵ ![]() ,∴f'(1)=1.
,∴f'(1)=1.
∴直線l的斜率為1,且與函數f(x)的圖象的切點坐標為(1,0).
∴直線l的方程為y=x﹣1.
又∵直線l與函數y=g(x)的圖象相切,
∴方程組  有一解.
有一解.
由上述方程消去y,并整理得x2+2(m﹣1)x+9=0①
依題意,方程①有兩個相等的實數根,
∴△=[2(m﹣1)]2﹣4×9=0
解之,得m=4或m=﹣2
∵m<0,∴m=﹣2.
(2)解:由(1)可知 ![]() ,
,
∴g'(x)=x﹣2∴h(x)=ln(x+1)﹣x+2(x>﹣1).
∴ ![]() .(7分)
.(7分)
∴當x∈(﹣1,0)時,h'(x)>0,當x∈(0,+∞)時,h'(x)<0.
∴當x=0時,h(x)取最大值,其最大值為2
(3)解:f(a+b)﹣f(2a)=ln(a+b)﹣ln2a=ln ![]() =ln(1+
=ln(1+ ![]() ).
).
∵0<b<a,∴﹣a,∴ ![]() .
.
由(2)知當x∈(﹣1,0)時,h(x)<h(0)∴當x∈(﹣1,0)時,ln(1+x)<x,
ln(1+ ![]() )<
)< ![]() .∴f(a+b)﹣f(2a)<
.∴f(a+b)﹣f(2a)< ![]()
【解析】(1)先根據導數的幾何意義求出函數在x=1處的導數,得到切線的斜率,再利用點斜式方程求出切線方程,最后將切線方程與 ![]() 聯立方程組,使方程組只有一解,利用判別式建立等量關系,求出m即可;(2)先求出h(x)的解析式,根據極值與最值的求解方法,將f(x)的各極值與其端點的函數值比較,其中最大的一個就是最大值;(3)f(a+b)﹣f(2a)=ln(a+b)﹣ln2a=ln
聯立方程組,使方程組只有一解,利用判別式建立等量關系,求出m即可;(2)先求出h(x)的解析式,根據極值與最值的求解方法,將f(x)的各極值與其端點的函數值比較,其中最大的一個就是最大值;(3)f(a+b)﹣f(2a)=ln(a+b)﹣ln2a=ln ![]() =ln(1+
=ln(1+ ![]() ).由(2)知當x∈(﹣1,0)時,h(x)<h(0)由ln(1+x)<x,
).由(2)知當x∈(﹣1,0)時,h(x)<h(0)由ln(1+x)<x,
ln(1+ ![]() )<
)< ![]() 即可得出f(a+b)﹣f(2a)<
即可得出f(a+b)﹣f(2a)< ![]() .
.
【考點精析】根據題目的已知條件,利用函數的最大(小)值與導數和不等式的證明的相關知識可以得到問題的答案,需要掌握求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值;不等式證明的幾種常用方法:常用方法有:比較法(作差,作商)、綜合法、分析法;其它方法有:換元法、反證法、放縮法、構造法,函數單調性法,數學歸納法等.
比較,其中最大的是一個最大值,最小的是最小值;不等式證明的幾種常用方法:常用方法有:比較法(作差,作商)、綜合法、分析法;其它方法有:換元法、反證法、放縮法、構造法,函數單調性法,數學歸納法等.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】設f(x)=﹣ ![]() x3+
x3+ ![]() x2+2ax.
x2+2ax.
(1)若f(x)在( ![]() ,+∞)上是單調減函數,求實數a的取值范圍.
,+∞)上是單調減函數,求實數a的取值范圍.
(2)當0<a<2時,f(x)在[1,4]上的最小值為﹣ ![]() ,求f(x)在該區間的最大值.
,求f(x)在該區間的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
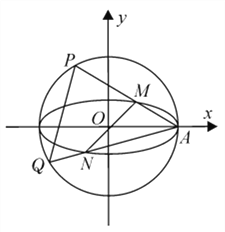
【題目】在平面直角坐標系![]() 中,已知圓
中,已知圓![]() ,橢圓
,橢圓![]() ,
, ![]() 為橢圓
為橢圓![]() 的右頂點,過原點且異于
的右頂點,過原點且異于![]() 軸的直線與橢圓
軸的直線與橢圓![]() 交于
交于![]() 兩點,
兩點, ![]() 在
在![]() 軸的上方,直線
軸的上方,直線![]() 與圓
與圓![]() 的另一交點為
的另一交點為![]() ,直線
,直線![]() 與圓
與圓![]() 的另一交點為
的另一交點為![]() ,
,
(1)若![]() ,求直線
,求直線![]() 的斜率;
的斜率;
(2)設![]() 與
與![]() 的面積分別為
的面積分別為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知不過第二象限的直線l:ax﹣y﹣4=0與圓x2+(y﹣1)2=5相切.
(1)求直線l的方程;
(2)若直線l1過點(3,﹣1)且與直線l平行,直線l2與直線l1關于直線y=1對稱,求直線l2的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AF=BF,EC∥FD,FD⊥底面ABCD,M是AB的中點. 
(1)求證:平面CFM⊥平面BDF;
(2)點N在CE上,EC=2,FD=3,當CN為何值時,MN∥平面BEF.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)是定義在R上的偶函數,對x∈R,都有f(x﹣2)=f(x+2),且當x∈[﹣2,0]時,f(x)=( ![]() )x﹣1,若在區間(﹣2,6]內關于x的方程f(x)﹣loga(x+2)=0(a>1)恰有3個不同的實數根,則a的取值范圍是( )
)x﹣1,若在區間(﹣2,6]內關于x的方程f(x)﹣loga(x+2)=0(a>1)恰有3個不同的實數根,則a的取值范圍是( )
A.(2,3)
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com