【題目】某中學為了組建一支業余足球隊，在高一年級隨機選取50名男生測量身高，發現被測男生的身高全部在160cm到184cm之間，將測量結果按如下方式分成六組：第1組
，第2組
，...，第6組
，如圖是按上述分組得到的頻率分布直方圖，以頻率近似概率.
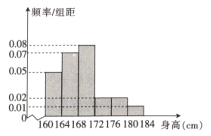
（1）若學校要從中選1名男生擔任足球隊長，求被選取的男生恰好在第5組或第6組的概率；
（2）現在從第5與第6組男生中選取兩名同學擔任守門員，求選取的兩人中最多有1名男生來自第5組的概率.
科目：高中數學 來源： 題型：
【題目】市面上有某品牌
型和
型兩種節能燈，假定型節能燈使用壽命都超過5000小時，經銷商對型節能燈使用壽命進行了調查統計，得到如下頻率分布直方圖：
某商家因原店面需要重新裝修，需租賃一家新店面進行周轉，合約期一年.新店面需安裝該品牌節能燈5支（同種型號）即可正常營業.經了解，型20瓦和型55瓦的兩種節能燈照明效果相當，都適合安裝.已知型和型節能燈每支的價格分別為120元、25元，當地商業電價為0.75元/千瓦時.假定該店面一年周轉期的照明時間為3600小時，若正常營業期間燈壞了立即購買同型燈管更換.（用頻率估計概率）
（Ⅰ）根據頻率直方圖估算型節能燈的平均使用壽命；
（Ⅱ）根據統計知識知，若一支燈管一年內需要更換的概率為
，那么
支燈管估計需要更換
支.若該商家新店面全部安裝了型節能燈，試估計一年內需更換的支數；
（Ⅲ）若只考慮燈的成本和消耗電費，你認為該商家應選擇哪種型號的節能燈，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司為了解共享單車的使用情況，隨機問卷50名使用者，然后根據這50名的問卷評分數據，統計得到如圖所示的頻率分布直方圖，其統計數據分組區間為[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]．
（1）求頻率分布直方圖中a的值；
（2）求這50名問卷評分數據的中位數；
（3）估計樣本的平均數．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某快遞公司收取快遞費用的標準是：重量不超過
的包裹收費
元；重量超過的包裹，除收費元之外，超過的部分，每超出（不足時按計算）需再收
元．公司從承攬過的包裹中，隨機抽取
件，其重量統計如下：
公司又隨機抽取了
天的攬件數，得到頻數分布表如下：
以記錄的天的攬件數的頻率作為各攬件數發生的概率
計算該公司
天中恰有
天攬件數在
的概率；
估計該公司對每件包裹收取的快遞費的平均值；
公司將快遞費的三分之一作為前臺工作人員的工資和公司利潤，剩余的用做其他費用，目前前臺有工作人員人，每人每天攬件不超過
件，每人每天工資元，公司正在考慮是否將前臺工作人員裁減
人，試計算裁員前后公司每日利潤的數學期望，并判斷裁員是否對提高公司利潤有利？（同一組中的攬件數以這組數據所在區間中點值作代表）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】高三年級有500名學生，為了了解數學科的學習情況，現從中隨機抽出若干名學生在一次測試中的數學成績，制成如下頻率分布表：
分組 | 頻數 | 頻率 |
|
|
|
|
| |
|
| |
| 12 |
|
|
| |
| 4 |
|
|
| |
合計 |
|
根據上面圖表，求
處的數值
在所給的坐標系中畫出
的頻率分布直方圖；
根據題中信息估計總體平均數，并估計總體落在
中的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】以下四個命題：
①“若
，則
”的逆否命題為真命題
②“
”是“函數
在區間
上為增函數”的充分不必要條件
③若
為假命題，則
，
均為假命題
④對于命題：
，
，則
為：
，
其中真命題的個數是（ ）
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某教育部門為了了解某地區高中學生校外補課的情況，隨機抽取了該地區100名學生進行調查，其中女生50人，將周補課時間不低于4小時的學生稱為“補課迷”.已知“補課迷”中有10名女生，右邊是根據調查樣本結果繪制的學生校外周補課時間的頻率分布直方圖（時間單位為：小時）.
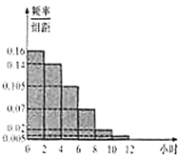
（1）根據調查樣本的結果估計該地區高中學生每周課外補課的平均時間（說明：同一組中的數據用該組區間的中間值作代表）；
（2）根據已知條件完成下面的
列聯表，根據調查資料你是否有
的把握認為“補課迷”與性別有關？
非補課迷 | 補課迷 | 合計 | |
男 | |||
女 | |||
合計 |
（3）將周補課時間不低于8小時者稱為“超級補課迷”，已知調查樣本中，有2名“超級補課迷”是女生，若從“超級補課迷”中任意選取3人，求至多有1名女學生的概率.
附：
.
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】橢圓
上動點
到兩個焦點的距離之和為4，且到右焦點距離的最大值為
．
(1)求橢圓
的方程；
(2)設點
為橢圓的上頂點，若直線
與橢圓交于兩點
（不是上下頂點）
．試問：直線是否經過某一定點，若是，求出該定點的坐標；若不是，請說明理由；
(3)在(2)的條件下，求
面積的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，底面
是邊長為2的菱形，
，
，平面
平面，點
為棱
的中點．
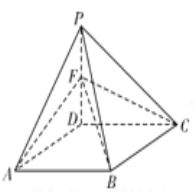
（Ⅰ）在棱
上是否存在一點
，使得
平面
，并說明理由；
（Ⅱ）當二面角
的余弦值為
時，求直線
與平面所成的角．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
