
【題目】已知函數![]() .
.
(Ⅰ)討論函數![]() 的單調性;
的單調性;
(Ⅱ)當![]() 時,
時,![]() 在定義域內恒成立,求實數
在定義域內恒成立,求實數![]() 的值.
的值.
【答案】(Ⅰ)當![]() 時,單調遞增區間為
時,單調遞增區間為![]() ,無單調遞減區間;當
,無單調遞減區間;當![]() 時,單調遞增區間為
時,單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]()
(Ⅱ)![]()
【解析】
(Ⅰ)求出函數![]() 的的定義域以及導函數,分類討論
的的定義域以及導函數,分類討論![]() ,
,![]() ,
,![]() 情況下導數的正負,由此得到答案;
情況下導數的正負,由此得到答案;
(Ⅱ)結合(Ⅰ)可得函數![]() 的最小值,要使
的最小值,要使![]() 在定義域內恒成立,則
在定義域內恒成立,則![]() 恒成立,令
恒成立,令![]() ,利用導數求出
,利用導數求出![]() 的最值,從而得到實數
的最值,從而得到實數![]() 的值。
的值。
(Ⅰ)由題可得函數![]() 的的定義域為
的的定義域為![]() ,
,![]() ;
;
(1) 當![]() 時,
時,![]() 恒成立,則
恒成立,則![]() 單調遞增區間為
單調遞增區間為![]() ,無單調遞減區間
,無單調遞減區間
(2) 當![]() 時,
時,![]() 恒成立,則
恒成立,則![]() 單調遞增區間為
單調遞增區間為![]() ,無單調遞減區間;
,無單調遞減區間;
(3) 當![]() 時,令
時,令![]() ,解得:
,解得:![]() ,令
,令![]() ,解得:
,解得:![]() ,則
,則![]() 單調遞增區間為
單調遞增區間為![]() ,
,![]() 單調遞減區間為
單調遞減區間為![]() ;
;
綜述所述:當![]() 時,單調遞增區間為
時,單調遞增區間為![]() ,無單調遞減區間;當
,無單調遞減區間;當![]() 時,單調遞增區間為
時,單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() ;
;
(Ⅱ)由(Ⅰ)可知,當![]() 時,
時,![]() 單調遞增區間為
單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() ,則
,則![]() ;
;
所以![]() 在定義域內恒成立,則
在定義域內恒成立,則![]() 恒成立,即
恒成立,即![]() ,
,
令![]() ,先求
,先求![]() 的最大值:
的最大值:![]() ,令
,令![]() ,解得:
,解得:![]() ,令
,令![]() ,解得:
,解得:![]() ,令
,令![]() ,解得:
,解得:![]() ,所以
,所以![]() 的單調增區間為
的單調增區間為![]() ,單調減區間為
,單調減區間為![]() ,則
,則![]()
所以當![]() 時,
時,![]() 恒成立,即
恒成立,即![]() 在定義域內恒成立,
在定義域內恒成立,
故答案為![]()


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知某中學高一、高二、高三三個年級的青年學生志愿者人數分別為180,120,60,現采用分層抽樣的方法從中抽取6名同學去森林公園風景區參加“保護鳥禽,愛我森林”宣傳活動.
(1)應從高一、高二、高三三個年級的學生志愿者中分別抽取多少人?
(2)設抽取的6名同學分別用A,B,C,D,E,F表示,現從中隨機抽取2名學生承擔分發宣傳材料的工作設事件M=“抽取的2名學生來自高一年級”,求事件M發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】工廠車間某部門有8個小組,在一次技能考試中成績情況分析如下:
小組 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
大于90分人數 | 6 | 6 | 7 | 3 | 5 | 3 | 3 | 7 |
不大于90分人數 | 39 | 39 | 38 | 42 | 40 | 42 | 42 | 38 |
(1)求90分以上人數![]() 對小組序號
對小組序號![]() 的線性回歸方程;
的線性回歸方程;
附:回歸方程為![]() ,其中
,其中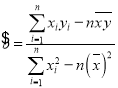 ,
,![]() .本題
.本題![]() ,
,![]() .
.
(2)能否在犯錯誤的概率不超過0.01的前提下認為7組與8組的成績是否優秀(大于90分)與小組有關系.附部分臨界值表:
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
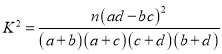 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解共享單車在![]() 市的使用情況,某調查機構借助網絡進行了問卷調查,并從參與調查的網友中隨機抽取了
市的使用情況,某調查機構借助網絡進行了問卷調查,并從參與調查的網友中隨機抽取了![]() 人進行分析,得到如下列聯表(單位:人).
人進行分析,得到如下列聯表(單位:人).
經常使用 | 偶爾使用或不使用 | 合計 | |
|
|
|
|
|
|
|
|
合計 |
|
|
|
(1)根據以上數據,能否在犯錯誤的概率不超過![]() 的前提下認為
的前提下認為![]() 市使用共享單車的情況與年齡有關;
市使用共享單車的情況與年齡有關;
(2)(i)現從所選取的![]() 歲以上的網友中,采用分層抽樣的方法選取
歲以上的網友中,采用分層抽樣的方法選取![]() 人,再從這
人,再從這![]() 人中隨機選出
人中隨機選出![]() 人贈送優惠券,求選出的
人贈送優惠券,求選出的![]() 人中至少有
人中至少有![]() 人經常使用共享單車的概率;
人經常使用共享單車的概率;
(ii)將頻率視為概率,從![]() 市所有參與調查的網友中隨機選取
市所有參與調查的網友中隨機選取![]() 人贈送禮品,記其中經常使用共享單車的人數為
人贈送禮品,記其中經常使用共享單車的人數為![]() ,求
,求![]() 的數學期望和方差.
的數學期望和方差.
參考公式: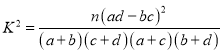 ,其中
,其中![]() .
.
參考數據:
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,幾何體EF-ABCD中,四邊形CDEF是正方形,四邊形ABCD為直角梯形,AB∥CD,AD⊥DC,△ACB是腰長為2![]() 的等腰直角三角形,平面CDEF⊥平面ABCD.
的等腰直角三角形,平面CDEF⊥平面ABCD.
(1)求證:BC⊥AF;
(2)求幾何體EF-ABCD的體積.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某人在塔的正東方向沿著南偏西60°的方向前進40 m以后,望見塔在東北方向上,若沿途測得塔的最大仰角為30°,則塔高為________________m.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓M:![]() =1(a>b>c)的一個頂點坐標為(0,1),焦距為2
=1(a>b>c)的一個頂點坐標為(0,1),焦距為2![]() .若直線y=x+m與橢圓M有兩個不同的交點A,B
.若直線y=x+m與橢圓M有兩個不同的交點A,B
(I)求橢圓M的方程;
(II)將![]() 表示為m的函數,并求△OAB面積的最大值(O為坐標原點)
表示為m的函數,并求△OAB面積的最大值(O為坐標原點)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com