
【題目】為了支援地震災區,某市要將一批救災物資運往災區,運輸公司準備使用甲、乙兩種貨車分三次完成此項任務,如果每輛車運的物資都正好達到保證安全的最大運載量,且前兩次運輸的情況如下表:

(1)甲、乙兩種貨車的最大運載量分別為多少噸?
(2)已知第三次使用了3輛甲種貨車和4輛乙種貨車剛好運完這批物資,問:第三次的物資共有多少噸?
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+bx+c(a≠0)的圖象過點(﹣1,2)且與x軸交點的橫坐標分別為x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列結論:①4a﹣2b+c<0;②2a﹣b<0;③b2+8a>4ac;④abc>0,其中正確的有( ).
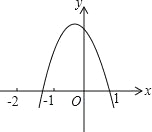
A.1個 B.2個 C.3個 D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小紅星期天從家里出發騎車去舅舅家做客,當她騎了一段路時,想起要買個禮物送給表弟,于是又折回到剛經過的一家商店,買好禮物后又繼續騎車去舅舅家,以下是她本次去舅舅家所用的時間與路程的關系式示意圖.根據圖中提供的信息回答下列問題: 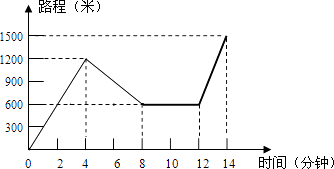
(1)小紅家到學校的路程是米,小紅在商店停留了分鐘;
(2)在整個去舅舅家的途中哪個時間段小紅騎車速度最快,最快的速度是多少米/分?
(3)本次去舅舅家的行程中,小紅一共行駛了多少米?一共用了多少分鐘?
查看答案和解析>>
科目:初中數學 來源: 題型:
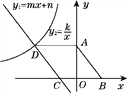
【題目】如圖,在菱形ABCD中,AD∥x軸,點A的坐標為(0,4),點B的坐標為(3,0).CD邊所在直線y1=mx+n與x軸交于點C,與雙曲線y2=![]() (x<0)交于點D.
(x<0)交于點D.
(1)求直線CD對應的函數表達式及k的值.
(2)把菱形ABCD沿y軸的正方向平移多少個單位后,點C落在雙曲線y2=![]() (x<0)上?
(x<0)上?
(3)直接寫出使y1>y2的自變量x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是芳芳設計的自由轉動的轉盤,上面寫有10個有理數。想想看,轉得下列各數的概率是多少?
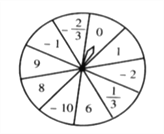
(1)轉得正數;
(2)轉得正整數;
(3)轉得絕對值小于6的數;
(4)轉得絕對值大于等于8的數。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明某天上午9時騎自行車離開家,15時回家,他有意描繪了離家的距離與時間的變化情況(如圖所示) 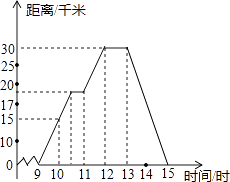
(1)圖象表示了哪兩個變量的關系?哪個是自變量?哪個是因變量?
(2)10時和13時,他分別離家多遠?
(3)他到達離家最遠的地方是什么時間?離家多遠?
(4)11時到12時他行駛了多少千米?
(5)他可能在哪段時間內休息,并吃午餐?
(6)他由離家最遠的地方返回時的平均速度是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
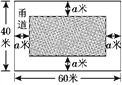
【題目】如圖①,為美化校園環境,某校計劃在一塊長為60米,寬為40米的長方形空地上,修建一個長方形花圃,并將花圃四周余下的空地修建成同樣寬的甬道,設甬道的寬為a米.
 ①
①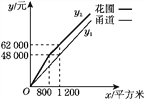 ②
②
(1)用含a的式子表示花圃的面積;
(2)如果甬道所占面積是整個長方形空地面積的![]() ,求此時甬道的寬;
,求此時甬道的寬;
(3)已知某園林公司修建甬道、花圃的造價y1(元)、y2(元)與修建面積x(平方米)之間的函數關系如圖②所示.如果學校決定由該公司承建此項目,并要求修建的甬道寬不少于2米且不超過10米,那么甬道的寬為多少米時,修建的甬道和花圃的總造價最低?最低總造價為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列各數中,是近似數的是( )。
A.七(1)班共有65名同學
B.足球比賽每方共有11名球員
C.光速是300000000米/秒
D.小王比小華多2元
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com