
【題目】港珠澳大橋(英文名稱:Hong Kong-Zhuhai-Macao Bridge)是中國境內一座連接香港、廣東珠海和澳門的橋隧工程,位于中國廣東省珠江口伶洋海域內,為珠江三角洲地區環線高速公路南環段.港珠澳大橋于![]() 年
年![]() 月
月![]() 日動工建設;于
日動工建設;于![]() 年
年![]() 月
月![]() 日實現主體工程全線貫通;于
日實現主體工程全線貫通;于![]() 年
年![]() 月
月![]() 日完成主體工程驗收;同年
日完成主體工程驗收;同年![]() 月
月![]() 日上午
日上午![]() 時開通運營.廣東某校數學“綜合與實踐”小組的同學把“測量港珠澳大橋某一段斜拉索頂端到橋面的距離”作為一項課題活動,他們制訂了測量方案,并利用課余時間完成該橋斜拉索實地測量,測量結果如下表
時開通運營.廣東某校數學“綜合與實踐”小組的同學把“測量港珠澳大橋某一段斜拉索頂端到橋面的距離”作為一項課題活動,他們制訂了測量方案,并利用課余時間完成該橋斜拉索實地測量,測量結果如下表
項目 | 內容 | ||
課題 | 測量港珠澳大橋某一段斜拉索頂端到橋面的距離 | ||
測量示意圖 |
| 說明:兩側斜拉索 | |
測量數據 |
|
|
|
|
|
| |
|
| ||

(1)請幫助該小組根據上表中的測量數據,求斜拉索頂端點![]() 到
到![]() 的距離(參考數據:
的距離(參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
(2)該小組要寫出一份完整的課題活動報告,除上表的項目外,你認為還需要補充哪些項目(寫出一個即可)?
 綜合自測系列答案
綜合自測系列答案科目:初中數學 來源: 題型:
【題目】某印刷廠每五年需淘汰一批同款的舊打印機并購買新機.購買新機時,若同時配買墨盒,每盒![]() 元,且最多可配買
元,且最多可配買![]() 盒;若非同時配買,則每盒需
盒;若非同時配買,則每盒需![]() 元.根據該廠以往的記錄,
元.根據該廠以往的記錄,![]() 臺同款打印機正常工作五年消耗的墨盒數如下表:
臺同款打印機正常工作五年消耗的墨盒數如下表:

(1)以這![]() 臺打印機五年消耗的墨盒數為樣本,估計“一臺該款打印機正常工作五年消耗的墨盒數不大于
臺打印機五年消耗的墨盒數為樣本,估計“一臺該款打印機正常工作五年消耗的墨盒數不大于![]() ”的概率;
”的概率;
(2)如果每臺打印機購買新機時配買的墨盒只能供本機使用,試以這![]() 臺打印機消耗墨盒費用的平均數作為決策依據,說明購買
臺打印機消耗墨盒費用的平均數作為決策依據,說明購買![]() 臺該款打印機時,應同時配買
臺該款打印機時,應同時配買![]() 盒還是
盒還是![]() 盒墨?
盒墨?
查看答案和解析>>
科目:初中數學 來源: 題型:
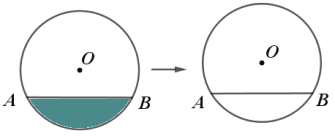
【題目】如圖,![]() 是一個圓柱體污水管道的橫截面,管道中有部分污水,污水液面橫截面寬度(即
是一個圓柱體污水管道的橫截面,管道中有部分污水,污水液面橫截面寬度(即![]() 長)為
長)為![]() 污水管道直徑為
污水管道直徑為![]() 則弦
則弦![]() 所對圓周角的大小為_____________________
所對圓周角的大小為_____________________![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點![]() 在直線
在直線![]() 上,過點
上,過點![]() 作
作![]() 軸于點
軸于點![]() ,作等腰直角三角形
,作等腰直角三角形![]() (
(![]() 與原點
與原點![]() 重合),再以
重合),再以![]() 為腰作等腰直角三角形
為腰作等腰直角三角形![]() ,以
,以![]() 為腰作等腰直角三角形
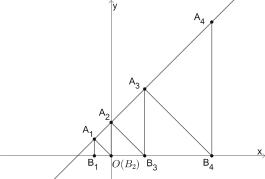
為腰作等腰直角三角形![]() ,…按照這樣的規律進行下去,那么
,…按照這樣的規律進行下去,那么![]() 的坐標為( )
的坐標為( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“普洱茶”是云南有名的特產,某網店專門銷售某種品牌的普洱茶,成本為30元/盒,每天銷售![]() (件)與銷售單價
(件)與銷售單價![]() (元)之間存在一次函數關系,如圖所示.
(元)之間存在一次函數關系,如圖所示.
(1)求![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(2)如果規定每天該種普洱茶的銷售量不低于240盒,該網店店主熱心公益事業,決定從每天的銷售利潤中捐出500元給扶貧基金會,當銷售單價為多少元時,每天獲取的凈利潤最大,最大凈利潤是多少?(注:凈利潤=總利潤-捐款)
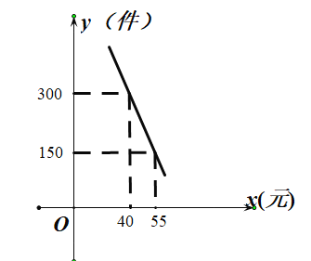
查看答案和解析>>
科目:初中數學 來源: 題型:
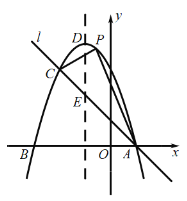
【題目】如圖,已知拋物線![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點,過點
兩點,過點![]() 的直線
的直線![]() 與拋物線交于點
與拋物線交于點![]() ,其中點
,其中點![]() 的坐標是
的坐標是![]() ,點
,點![]() 的坐標是
的坐標是![]() ,拋物線的頂點為點
,拋物線的頂點為點![]() .
.
(1)求拋物線和直線![]() 的解析式.
的解析式.
(2)若點![]() 是拋物線上位于直線
是拋物線上位于直線![]() 上方的一個動點,求
上方的一個動點,求![]() 的面積的最大值及此時點
的面積的最大值及此時點![]() 的坐標.
的坐標.
(3)若拋物線的對稱軸與直線![]() 相交于點
相交于點![]() ,點
,點![]() 為直線
為直線![]() 上的任意一點,過點
上的任意一點,過點![]() 作
作![]() 交拋物線于點
交拋物線于點![]() ,以
,以![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形能否為平行四邊形?若能,求出點
為頂點的四邊形能否為平行四邊形?若能,求出點![]() 的坐標;若不能,請說明理由.
的坐標;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 的與
的與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,
,
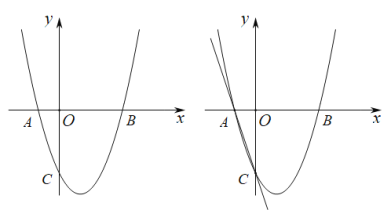
(1)求該拋物線的解析式及頂點的坐標;
(2)若![]() 是線段
是線段![]() 上一動點,過
上一動點,過![]() 作
作![]() 軸的平行線交拋物線于點
軸的平行線交拋物線于點![]() ,交
,交![]() 于點
于點![]() ,設
,設![]() 時,
時,![]() 的面積為
的面積為![]() .求
.求![]() 關于
關于![]() 的函數關系式;若
的函數關系式;若![]() 有最大值,請求出
有最大值,請求出![]() 的最大值,若沒有,請說明理由;
的最大值,若沒有,請說明理由;
(3)若![]() 是
是![]() 軸上一個動點,過
軸上一個動點,過![]() 作射線
作射線![]() 交拋物線于點
交拋物線于點![]() ,隨著
,隨著![]() 點的運動,在
點的運動,在![]() 軸上是否存在這樣的點
軸上是否存在這樣的點![]() ,使以
,使以 ![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形為平行四邊形?若存在,請直接寫出
為頂點的四邊形為平行四邊形?若存在,請直接寫出![]() 點的坐標;若不存在,請說明理由.
點的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某海域有A、B、C三艘船正在捕魚作業,C船突然出現故障,向A、B兩船發出緊急求救信號,此時B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏東33°方向,同時又位于B船的北偏東78°方向.
(1)求∠ABC的度數;
(2)A船以每小時30海里的速度前去救援,問多長時間能到出事地點.(結果精確到0.01小時).
(參考數據:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中數學 來源: 題型:
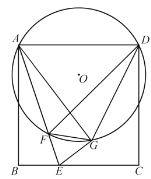
【題目】在正方形ABCD中,點E是BC邊上一動點,連接AE,沿AE將△ABE翻折得△AGE,連接DG,作△AGD的外接⊙O,⊙O交AE于點F,連接FG、FD.
(1)求證∠AGD=∠EFG;
(2)求證△ADF∽△EGF;
(3)若AB=3,BE=1,求⊙O的半徑.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com