Question

【題目】已知拋物線E：的準線為，焦點為，為坐標原點。

（1）求過點、，且與相切的圓的方程；

（2）過點的直線交拋物線E于兩點，點A關于x軸的對稱點為，且點與點不重合，求證：直線過定點.

Answer 1

【答案】（1）（2）詳見解析

【解析】

（1）由題意求得焦點及準線方程，即可求得圓心，利用點到直線的距離公式，即可求得半徑，即可求得圓的方程；

（2）設直線AB方程為y＝k（x﹣1），代入橢圓方程，利用韋達定理，求得直線BA′的方程為，當y＝0，求得x＝﹣1，則直線BA′過定點（﹣1，0）；

（1）拋物線E：y2＝4x的準線l的方程為：x＝﹣1，焦點坐標為F（1，0），

設所求圓的圓心C（a，b），半徑為r，∵圓C過O，F，

∴，∵圓C與直線l：x＝﹣1相切，

∴．

由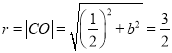，得．

∴過O，F，且與直線l相切的圓的方程為；

（2）依題意知直線AB的斜率存在，設直線AB方程為y＝k（x﹣1），A（x1，y1），B（x2，y2），（x1≠x2），A′（x1，﹣y1），

聯立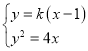，消去y得k2x2﹣（2k2+4）x+k2＝0．

∴，x1x2＝1．

∵直線BA′的方程為，又由對稱性可知：定點在x軸上，

∴令y＝0，得．

直線BA′過定點（﹣1，0），