
【題目】某地區在一次考試后,從全體考生中隨機抽取44名,獲取他們本次考試的數學成績(x)和物理成績(y),繪制成如圖散點圖:
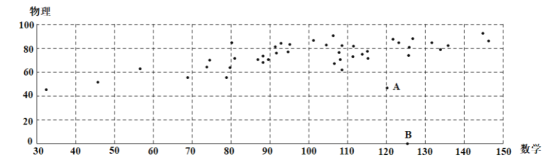
根據散點圖可以看出y與x之間有線性相關關系,但圖中有兩個異常點A,B.經調查得知,A考生由于重感冒導致物理考試發揮失常,B考生因故未能參加物理考試.為了使分析結果更科學準確,剔除這兩組數據后,對剩下的數據作處理,得到一些統計的值:![]()
![]()
![]() 其中xi,yi分別表示這42名同學的數學成績、物理成績,i=1,2,…,42,y與x的相關系數r=0.82.
其中xi,yi分別表示這42名同學的數學成績、物理成績,i=1,2,…,42,y與x的相關系數r=0.82.
(1)若不剔除A,B兩名考生的數據,用44組數據作回歸分析,設此時y與x的相關系數為r0.試判斷r0與r的大小關系,并說明理由;
(2)求y關于x的線性回歸方程(系數精確到0.01),并估計如果B考生加了這次物理考試(已知B考生的數學成績為125分),物理成績是多少?(精確到個位);
(3)從概率統計規律看,本次考試該地區的物理成績ξ服從正態分布![]() ,以剔除后的物理成績作為樣本,用樣本平均數
,以剔除后的物理成績作為樣本,用樣本平均數![]() 作為μ的估計值,用樣本方差s2作為σ2的估計值.試求該地區5000名考生中,物理成績位于區間(62.8,85.2)的人數Z的數學期望.
作為μ的估計值,用樣本方差s2作為σ2的估計值.試求該地區5000名考生中,物理成績位于區間(62.8,85.2)的人數Z的數學期望.
附:①回歸方程![]() 中:
中: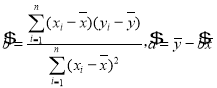
②若![]() ,則
,則![]()
③![]() 11.2
11.2
【答案】(1)r0<r,理由詳見解析;(2)![]() ,81分;(3)3413.
,81分;(3)3413.
【解析】
(1)結合散點圖,可得出結論;
(2)利用題中給的相關系數,最小二乘法寫出回歸直線方程,再令x=125,即可算出答案;
(3)算出![]() ,s2,得到ξ~N(74,125),
,s2,得到ξ~N(74,125),![]() 11.2,所以P(63.8<ξ<85.2)=
11.2,所以P(63.8<ξ<85.2)=![]() 因為
因為![]() ,即可算出期望.
,即可算出期望.
(1)r0<r.
理由如下:由圖可知,y與x成正相關關系,
①異常點 A,B 會降低變量之間的線性相關程度.
②44個數據點與其回歸直線的總偏差更大,回歸效果更差,所以相關系數更小.
③42個數據點與其回歸直線的總偏差更小,回歸效果更好,所以相關系數更大.
④42個數據點更貼近其回歸直線l.
⑤44個數據點與其回歸直線更離散.
(2)由題中數據可得:
![]() ,
,
所以![]() ,
,
又因為![]() ,所以
,所以 ,
,
![]() ,所以
,所以![]() ,
,
將![]() 代入,得
代入,得![]() ,
,
所以估計B同學的物理成績約為81分.
(3)![]() ,
,
所以ξ~N(74,125),又因為![]() 11.2
11.2
所以![]() ,
,
因為![]() ,所以
,所以![]() ,
,
即該地區本次考試物理成績位于區間(62.8,85.2)的數學期望為3413.


 手拉手全優練考卷系列答案
手拉手全優練考卷系列答案科目:高中數學 來源: 題型:
【題目】某商場春節期間推出一項優惠活動,活動規則如下:消費額每滿300元可轉動如圖所示的轉盤一次,并獲得相應金額的返券,假定指針等可能地停在任一位置.若指針停在區域Ⅰ返券60元;停在區域Ⅱ返券30元;停在區域Ⅲ不返券.例如:消費600元,可抽獎2次,所獲得的返券金額是兩次金額之和.
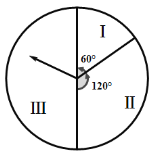
(Ⅰ)若某位顧客消費300元,求返券金額不低于30元的概率;
(Ⅱ)若某位顧客恰好消費600元,并按規則參與了活動,他獲得返券的金額記為![]() (元).求隨機變量
(元).求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】雙曲線定位法是通過測定待定點到至少三個已知點的兩個距離差所進行的一種無線電定位.通過船(待定點)接收到三個發射臺的電磁波的時間差計算出距離差,兩個距離差即可形成兩條位置雙曲線,兩者相交便可確定船位.我們來看一種簡單的“特殊”狀況;如圖所示,已知三個發射臺分別為![]() ,
,![]() ,
,![]() 且剛好三點共線,已知
且剛好三點共線,已知![]() 海里,
海里,![]() 海里,現以
海里,現以![]() 的中點為原點,
的中點為原點,![]() 所在直線為
所在直線為![]() 軸建系.現根據船
軸建系.現根據船![]() 接收到
接收到![]() 點與
點與![]() 點發出的電磁波的時間差計算出距離差,得知船
點發出的電磁波的時間差計算出距離差,得知船![]() 在雙曲線
在雙曲線![]() 的左支上,根據船
的左支上,根據船![]() 接收到
接收到![]() 臺和
臺和![]() 臺電磁波的時間差,計算出船
臺電磁波的時間差,計算出船![]() 到
到![]() 發射臺的距離比到
發射臺的距離比到![]() 發射臺的距離遠30海里,則點
發射臺的距離遠30海里,則點![]() 的坐標(單位:海里)為( )
的坐標(單位:海里)為( )

A. B.
B.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】概率論起源于博弈游戲.17世紀,曾有一個“賭金分配“的問題:博弈水平相當的甲、乙兩人進行博弈游戲,每局比賽都能分出勝負,沒有平局.雙方約定,各出賭金48枚金幣,先贏3局者可獲得全部賭金;但比賽中途因故終止了,此時甲贏了2局,乙贏了1局.向這96枚金幣的賭金該如何分配?數學家費馬和帕斯卡都用了現在稱之為“概率“的知識,合理地給出了賭金分配方案.該分配方案是( )
A.甲48枚,乙48枚B.甲64枚,乙32枚
C.甲72枚,乙24枚D.甲80枚,乙16枚
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小芳、小明兩人各拿兩顆質地均勻的骰子做游戲,規則如下:若擲出的點數之和為4的倍數,則由原投擲人繼續投擲;若擲出的點數之和不是4的倍數,則由對方接著投擲.
(1)規定第1次從小明開始.
(ⅰ)求前4次投擲中小明恰好投擲2次的概率;
(ⅱ)設游戲的前4次中,小芳投擲的次數為![]() ,求隨機變量
,求隨機變量![]() 的分布列與期望.
的分布列與期望.
(2)若第1次從小芳開始,求第![]() 次由小芳投擲的概率
次由小芳投擲的概率![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,橢圓
中,橢圓![]() 經過點
經過點![]() ,且點
,且點![]() 與橢圓的左、右頂點連線的斜率之積為
與橢圓的左、右頂點連線的斜率之積為![]() .
.

(1)求橢圓![]() 的方程;
的方程;
(2)若橢圓![]() 上存在兩點
上存在兩點![]() ,使得
,使得![]() 的垂心(三角形三條高的交點)恰為坐標原點
的垂心(三角形三條高的交點)恰為坐標原點![]() ,試求直線
,試求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為F.
的右焦點為F.
(1)求點F的坐標和橢圓C的離心率;
(2)直線![]() 過點F,且與橢圓C交于P,Q兩點,如果點P關于x軸的對稱點為
過點F,且與橢圓C交于P,Q兩點,如果點P關于x軸的對稱點為![]() ,判斷直線
,判斷直線![]() 是否經過x軸上的定點,如果經過,求出該定點坐標;如果不經過,說明理由.
是否經過x軸上的定點,如果經過,求出該定點坐標;如果不經過,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com