
【題目】小芳、小明兩人各拿兩顆質地均勻的骰子做游戲,規則如下:若擲出的點數之和為4的倍數,則由原投擲人繼續投擲;若擲出的點數之和不是4的倍數,則由對方接著投擲.
(1)規定第1次從小明開始.
(ⅰ)求前4次投擲中小明恰好投擲2次的概率;
(ⅱ)設游戲的前4次中,小芳投擲的次數為![]() ,求隨機變量
,求隨機變量![]() 的分布列與期望.
的分布列與期望.
(2)若第1次從小芳開始,求第![]() 次由小芳投擲的概率
次由小芳投擲的概率![]() .
.
【答案】(1)(ⅰ)![]() (ⅱ)見解析,
(ⅱ)見解析,![]() (2)
(2)![]()
【解析】
(1)(ⅰ)一人投擲兩顆骰子,向上的點數之和為4的倍數的概為![]() ,前4次投擲中小明恰好投擲2次有三種情況:小明,小明,小芳,小芳;小明,小芳,小明,小芳;小明,小芳,小芳,小明,分別計算概率相加即可;(ⅱ)小芳投擲的次數
,前4次投擲中小明恰好投擲2次有三種情況:小明,小明,小芳,小芳;小明,小芳,小明,小芳;小明,小芳,小芳,小明,分別計算概率相加即可;(ⅱ)小芳投擲的次數![]() 的所有可能的取值為0,1,2,3,分別求出相應的概率即可;
的所有可能的取值為0,1,2,3,分別求出相應的概率即可;
(2)若第1次從小芳開始,則第![]() 次由小芳投擲骰子有兩種情況:1.第
次由小芳投擲骰子有兩種情況:1.第![]() 次由小芳投擲,第
次由小芳投擲,第![]() 次繼續由小芳投擲,2.第
次繼續由小芳投擲,2.第![]() 次由小明投擲,第
次由小明投擲,第![]() 次由小芳投擲.
次由小芳投擲.
(1)一人投擲兩顆骰子,向上的點數之和為4的倍數的概為![]() .
.
(ⅰ)因為第1次從小明開始,所以前4次投擲中小明恰好投擲2次的概率,
![]() .
.
(ⅱ)設游戲的前4次中,小芳投擲的次數為![]() ,依題意,
,依題意,![]() 可取0,1,2,3,
可取0,1,2,3,
所以![]() ,
,![]() ,
,
![]() ,
,![]() .
.
所以![]() 的分布列為
的分布列為
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以![]() .
.
(2)若第1次從小芳開始,則第![]() 次由小芳投擲骰子有兩種情況:
次由小芳投擲骰子有兩種情況:
①第![]() 次由小芳投擲,第
次由小芳投擲,第![]() 次繼續由小芳投擲,其概率為
次繼續由小芳投擲,其概率為![]() ;
;
②第![]() 次由小明投擲,第
次由小明投擲,第![]() 次由小芳投擲,
次由小芳投擲,
其概率為![]() .
.
因為①②兩種情形是互斥的,所以![]() ,
,
所以![]() .因為
.因為![]() ,所以
,所以![]() 是以
是以![]() 為首項,
為首項,
![]() 為公比的等比數列,所以
為公比的等比數列,所以![]() ,即
,即![]() .
.


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為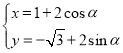 (其中
(其中![]() 為參數,
為參數,![]() ).在極坐標系(以坐標原點
).在極坐標系(以坐標原點![]() 為極點,以
為極點,以![]() 軸非負半軸為極軸)中,曲線
軸非負半軸為極軸)中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若曲線![]() 上恰有一個點到曲線
上恰有一個點到曲線![]() 的距離為1,求曲線
的距離為1,求曲線![]() 的直角坐標方程.
的直角坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() )的圖象的兩條相鄰對稱軸之間的距離為
)的圖象的兩條相鄰對稱軸之間的距離為![]() ,且圖象上一個最低點為
,且圖象上一個最低點為![]() .
.
(1)求函數![]() 的解析式;
的解析式;
(2)當![]() 時,求函數
時,求函數![]() 的值域;
的值域;
(3)若方程![]() 在
在![]() 上有兩個不相等的實數根
上有兩個不相等的實數根![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區在一次考試后,從全體考生中隨機抽取44名,獲取他們本次考試的數學成績(x)和物理成績(y),繪制成如圖散點圖:
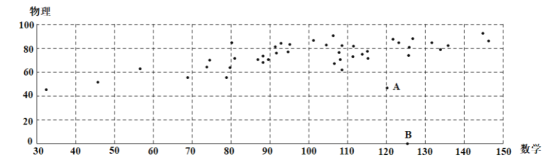
根據散點圖可以看出y與x之間有線性相關關系,但圖中有兩個異常點A,B.經調查得知,A考生由于重感冒導致物理考試發揮失常,B考生因故未能參加物理考試.為了使分析結果更科學準確,剔除這兩組數據后,對剩下的數據作處理,得到一些統計的值:![]()
![]()
![]() 其中xi,yi分別表示這42名同學的數學成績、物理成績,i=1,2,…,42,y與x的相關系數r=0.82.
其中xi,yi分別表示這42名同學的數學成績、物理成績,i=1,2,…,42,y與x的相關系數r=0.82.
(1)若不剔除A,B兩名考生的數據,用44組數據作回歸分析,設此時y與x的相關系數為r0.試判斷r0與r的大小關系,并說明理由;
(2)求y關于x的線性回歸方程(系數精確到0.01),并估計如果B考生加了這次物理考試(已知B考生的數學成績為125分),物理成績是多少?(精確到個位);
(3)從概率統計規律看,本次考試該地區的物理成績ξ服從正態分布![]() ,以剔除后的物理成績作為樣本,用樣本平均數
,以剔除后的物理成績作為樣本,用樣本平均數![]() 作為μ的估計值,用樣本方差s2作為σ2的估計值.試求該地區5000名考生中,物理成績位于區間(62.8,85.2)的人數Z的數學期望.
作為μ的估計值,用樣本方差s2作為σ2的估計值.試求該地區5000名考生中,物理成績位于區間(62.8,85.2)的人數Z的數學期望.
附:①回歸方程![]() 中:
中: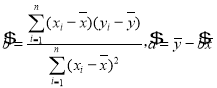
②若![]() ,則
,則![]()
③![]() 11.2
11.2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某人承包了一塊矩形土地![]() 用來種植草莓,其中
用來種植草莓,其中![]() m,
m,![]() m.現規劃建造如圖所示的半圓柱型塑料薄膜大棚
m.現規劃建造如圖所示的半圓柱型塑料薄膜大棚![]() 個,每個半圓柱型大棚的兩半圓形底面與側面都需蒙上塑料薄膜(接頭處忽略不計),塑料薄膜的價格為每平方米
個,每個半圓柱型大棚的兩半圓形底面與側面都需蒙上塑料薄膜(接頭處忽略不計),塑料薄膜的價格為每平方米![]() 元;另外,還需在每個大棚之間留下
元;另外,還需在每個大棚之間留下![]() m寬的空地用于建造排水溝與行走小路(如圖中
m寬的空地用于建造排水溝與行走小路(如圖中![]() m),這部分建設造價為每平方米
m),這部分建設造價為每平方米![]() 元.
元.
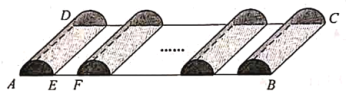
(1)當![]() 時,求蒙一個大棚所需塑料薄膜的面積;(本小題結果保留
時,求蒙一個大棚所需塑料薄膜的面積;(本小題結果保留![]() )
)
(2)試確定大棚的個數,使得上述兩項費用的和最低?(本小題計算中![]() 取
取![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種質地均勻的正四面體玩具的4個面上分別標有數字0,1,2,3,將這個玩具拋擲![]() 次,記第
次,記第![]() 次拋擲后玩具與桌面接觸的面上所標的數字為
次拋擲后玩具與桌面接觸的面上所標的數字為![]() ,數列
,數列![]() 的前
的前![]() 和為
和為![]() .記
.記![]() 是3的倍數的概率為
是3的倍數的概率為![]() .
.
(1)求![]() ,
,![]() ;
;
(2)求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與曲線
,與曲線![]() 交于兩點
交于兩點![]() ,
,![]() .
.
(1)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,設拋物線![]() 的焦點為
的焦點為![]() ,
,![]() 是拋物線上一點,過點
是拋物線上一點,過點![]() 的切線
的切線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,
,![]() 是線段
是線段![]() 的中點.直線
的中點.直線![]() 交拋物線于另一點
交拋物線于另一點![]() .
.
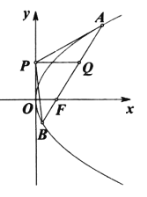
(1)求證:![]() 垂直于
垂直于![]() 軸;
軸;
(2)求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com