
【題目】法國數學家龐加是個喜歡吃面包的人,他每天都會購買一個面包,面包師聲稱自己出售的每個面包的平均質量是1000![]() ,上下浮動不超過50
,上下浮動不超過50![]() .這句話用數學語言來表達就是:每個面包的質量服從期望為1000
.這句話用數學語言來表達就是:每個面包的質量服從期望為1000![]() ,標準差為50
,標準差為50![]() 的正態分布.
的正態分布.
(1)假設面包師的說法是真實的,從面包師出售的面包中任取兩個,記取出的兩個面包中質量大于1000![]() 的個數為
的個數為![]() ,求
,求![]() 的分布列和數學期望;
的分布列和數學期望;
(2)作為一個善于思考的數學家,龐加萊每天都會將買來的面包稱重并記錄,25天后,得到數據如下表,經計算25個面包總質量為24468![]() .龐加萊購買的25個面包質量的統計數據(單位:
.龐加萊購買的25個面包質量的統計數據(單位:![]() )
)
981 | 972 | 966 | 992 | 1010 | 1008 | 954 | 952 | 969 | 978 |
989 | 1001 | 1006 | 957 | 952 | 969 | 981 | 984 | 952 | 959 |
987 | 1006 | 1000 | 977 | 966 |
盡管上述數據都落在![]() 上,但龐加菜還是認為面包師撒謊,根據所附信息,從概率角度說明理由
上,但龐加菜還是認為面包師撒謊,根據所附信息,從概率角度說明理由
附:
①若![]() ,從X的取值中隨機抽取25個數據,記這25個數據的平均值為Y,則由統計學知識可知:隨機變量
,從X的取值中隨機抽取25個數據,記這25個數據的平均值為Y,則由統計學知識可知:隨機變量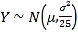
②若![]() ,則
,則![]() ,
,![]() ,
,![]() ;
;
③通常把發生概率在0.05以下的事件稱為小概率事件.
【答案】(1)分布列見解析;期望為1(個)(2)詳見解析
【解析】
(1)由題意知,![]() 的所有可能取值為0,1,2.可求得
的所有可能取值為0,1,2.可求得![]() ;
;![]() ;
;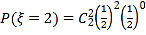 .從而可求得
.從而可求得![]() 的分布列和其數學期望.
的分布列和其數學期望.
(2)記面包師制作的每個面包的質量為隨機變量X.假設面包師沒有撒謊,則![]() .由附①,從X的取值中隨機抽取25個數據,記這25個數據的平均值為Y,則
.由附①,從X的取值中隨機抽取25個數據,記這25個數據的平均值為Y,則![]() .可求得這25個數據的平均值為
.可求得這25個數據的平均值為![]() ,而由由附②數據知,
,而由由附②數據知,![]() ,由附③知,事件“
,由附③知,事件“![]() ”為小概率事件,可得結論.
”為小概率事件,可得結論.
(1)由題意知,![]() 的所有可能取值為0,1,2.
的所有可能取值為0,1,2.
![]() ;
;![]() ;
;
![]() .所以
.所以![]() 的分布列為:
的分布列為:
| 0 | 1 | 2 |
P |
|
|
|
所以![]() (個).
(個).
(2)記面包師制作的每個面包的質量為隨機變量X.
假設面包師沒有撒謊,則![]() .
.
根據附①,從X的取值中隨機抽取25個數據,記這25個數據的平均值為Y,
則![]() .
.
龐加萊記錄的25個面包質量,相當于從X的取值中隨機抽取了25個數據,
這25個數據的平均值為![]() ,
,
由附②數據知,![]() ,
,
由附③知,事件“![]() ”為小概率事件,
”為小概率事件,
所以“假設面包師沒有撒謊”有誤,
所以龐加萊認為面包師撒謊.


科目:高中數學 來源: 題型:
【題目】唐朝的狩獵景象浮雕銀杯如圖1所示.其浮雕臨摹了國畫、漆繪和墓室壁畫,體現了古人的智慧與工藝.它的盛酒部分可以近似地看作是半球與圓柱的組合體(假設內壁表面光滑,忽略杯壁厚度),如圖2所示.已知球的半徑為R,酒杯內壁表面積為![]() ,設酒杯上部分(圓柱)的體積為
,設酒杯上部分(圓柱)的體積為![]() ,下部分(半球)的體積為
,下部分(半球)的體積為![]() ,則
,則![]() ( )
( )
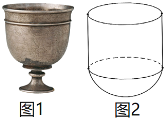
A.2B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在矩形![]() 中,
中,![]() 為邊
為邊![]() 的中點,將
的中點,將![]() 沿直線
沿直線![]() 翻轉成
翻轉成![]() (
(![]() 平面
平面![]() ).若
).若![]() 分別為線段
分別為線段![]() 的中點,則在
的中點,則在![]() 翻轉過程中,下列說法正確的是( )
翻轉過程中,下列說法正確的是( )
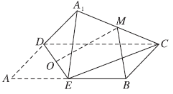
A.與平面![]() 垂直的直線必與直線
垂直的直線必與直線![]() 垂直
垂直
B.異面直線![]() 與
與![]() 所成的角是定值
所成的角是定值
C.一定存在某個位置,使![]()
D.三棱錐![]() 外接球半徑與棱
外接球半徑與棱![]() 的長之比為定值
的長之比為定值
查看答案和解析>>
科目:高中數學 來源: 題型:
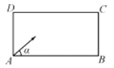
【題目】臺球運動已有五、六百年的歷史,參與者用球桿在臺上擊球.若和光線一樣,臺球在球臺上碰到障礙物后也遵從反射定律如圖,有一張長方形球臺ABCD,![]() ,現從角落A沿角
,現從角落A沿角![]() 的方向把球打出去,球經2次碰撞球臺內沿后進入角落C的球袋中,則
的方向把球打出去,球經2次碰撞球臺內沿后進入角落C的球袋中,則![]() 的值為( )
的值為( )
A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=ex+asinx,x∈(-π,+∞),下列說法正確的是( )
A.當a=1時,f(x)在(0,f(0))處的切線方程為2x-y+1=0
B.當a=1時,f(x)存在唯一極小值點x0且-1<f(x0)<0
C.對任意a>0,f(x)在(-π,+∞)上均存在零點
D.存在a<0,f(x)在(-π,+∞)上有且只有一個零點
查看答案和解析>>
科目:高中數學 來源: 題型:
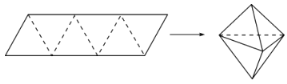
【題目】農歷五月初五是端午節,民間有吃粽子的習慣,粽子又稱粽粒,古稱角黍,是端午節大家都會品嘗的食品.如圖,平行四邊形形狀的紙片是由六個邊長為2的正三角形構成的,將它沿虛線折起來,可以得到如圖所示粽子形狀的六面體,則該六面體的體積為_________;若該六面體內有一球,當該球體積最大時,球的表面積是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“二進制”來源于我國古代的《易經》,該書中有兩類最基本的符號:“─”和“﹣﹣”,其中“─”在二進制中記作“1”,“﹣﹣”在二進制中記作“0”.如符號“”對應的二進制數011(2)化為十進制的計算如下:011(2)=0×22+1×21+1×20=3(10).若從兩類符號中任取2個符號進行排列,則得到的二進制數所對應的十進制數大于2的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com