【題目】遼寧號航母紀(jì)念章從2012年10月5日起開始上市，通過市場調(diào)查，得到該紀(jì)念章每1枚的市場價y（單位：元）與上市時間x（單位：天）的數(shù)據(jù)如下：
上市時間x天 | 8 | 10 | 32 |
市場價y元 | 82 | 60 | 82 |
（1）根據(jù)上表數(shù)據(jù)，從下列函數(shù)中選取一個恰當(dāng)?shù)暮瘮?shù)描述遼寧號航母紀(jì)念章的市場價y與上市時間x的變化關(guān)系并說明理由：①
；②
；③
.
（2）利用你選取的函數(shù)，求遼寧號航母紀(jì)念章市場價最低時的上市天數(shù)及最低的價格.
【答案】（1）
，理由見解析；（2）遼寧號航母紀(jì)念章市場價最低時的上市天數(shù)為20天，最低的價格為10元．
【解析】
（1）根據(jù)圖中數(shù)據(jù)，隨著時間
的增加，
的值先減后增，結(jié)合函數(shù)的單調(diào)性即可得出結(jié)論；
（2）把點代入中，解出參數(shù)求出解析式，即可求解遼寧號航母紀(jì)念章市場價最低時的上市天數(shù)及最低的價格.
（1）∵隨著時間x的增加，y的值先減后增，而所給的三個函數(shù)中
和
顯然都是單調(diào)函數(shù)，不滿足題意，
．
（2）把點代入中，
得
解得
∴
，
∴當(dāng)
時，y有最小值
．
答：遼寧號航母紀(jì)念章市場價最低時的上市天數(shù)為20天，最低的價格為10元．
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如表提供了某廠節(jié)能降耗技術(shù)改造后生產(chǎn)甲產(chǎn)品過程中記錄的產(chǎn)量
（噸）與相應(yīng)的生產(chǎn)能耗
（噸標(biāo)準(zhǔn)煤）的幾組對照數(shù)據(jù)
|
|
|
|
|
|
|
|
|
|
（1）請畫出上表數(shù)據(jù)的散點圖；
（2）請根據(jù)上表提供的數(shù)據(jù)，用最小二乘法求出關(guān)于的線性回歸方程
；
（3）已知該廠技改前100噸甲產(chǎn)品的生產(chǎn)能耗為90噸標(biāo)準(zhǔn)煤.試根據(jù)（2）求出的線性同歸方程，預(yù)測生產(chǎn)100噸甲產(chǎn)品的生產(chǎn)能耗比技改前降低多少噸標(biāo)準(zhǔn)煤?（參考數(shù)值
）
（附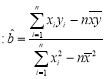
，
，其中
，
為樣本均值）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)
為非空實數(shù)集（至少有兩個元素），若對任意
，都有
，且
，則稱為封閉集，則下列四個判斷：
①集合為封閉集，則為無限集； ②集合
為封閉集；
③若集合
為封閉集，則
為封閉集； ④若為封閉集，則一定有
；，
其中正確的命題個數(shù)有（ ）.
A.4個B.3個C.2個D.1個
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知四棱錐
中，
平面ABCD，
，
，
，M是線段AB的中點.
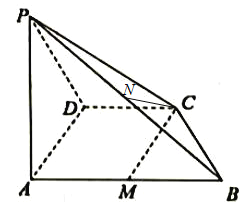
（1）求證：
平面PAB；
（2）已知點N是線段PB的中點，試判斷直線CN與平面PAD的位置關(guān)系，并證明你的判斷.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
.
（1）當(dāng)
時,求
的單調(diào)遞增區(qū)間；
（2）證明：當(dāng)
時，有兩個零點；
（3）若
，函數(shù)
在
處取得最小值，證明：
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】下列關(guān)于回歸分析的說法中錯誤的是（ ）
A. 回歸直線一定過樣本中心
B. 殘差圖中殘差點比較均勻地落在水平的帶狀區(qū)域中，說明選用的模型比較合適
C. 兩個模型中殘差平方和越小的模型擬合的效果越好
D. 甲、乙兩個模型的
分別約為0.98和0.80，則模型乙的擬合效果更好
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖所示，正四棱錐
中，
為底面正方形的中心，側(cè)棱
與底面
所成的角的正切值為
．
（1）求側(cè)面
與底面所成的二面角的大小；
（2）若
是
的中點，求異面直線
與
所成角的正切值；
（3）問在棱
上是否存在一點
，使
⊥側(cè)面
，若存在，試確定點的位置；若不存在，說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】
如圖，長方體ABCD–A1B1C1D1的底面ABCD是正方形，點E在棱AA1上，BE⊥EC1.
（1）證明：BE⊥平面EB1C1；
（2）若AE=A1E，求二面角B–EC–C1的正弦值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
