
【題目】在等腰直角三角形ABC中,AB=AC=4,點P是邊AB邊上異于AB的一點,光線從點P出發,經BC,CA反射后又回到點P(如圖),若光線QR經過△ABC的重心,則AP等于( )
A.2
B.1
C.![]()
D.![]()
【答案】D
【解析】解:建立如圖所示的坐標系:
可得B(4,0),C(0,4),故直線BC的方程為x+y=4,
△ABC的重心為( ![]() ,
, ![]() ),設P(a,0),其中0<a<4,
),設P(a,0),其中0<a<4,
則點P關于直線BC的對稱點P1(x,y),滿足 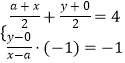 ,
,
解得 ![]() ,即P1(4,4﹣a),易得P關于y軸的對稱點P2(﹣a,0),
,即P1(4,4﹣a),易得P關于y軸的對稱點P2(﹣a,0),
由光的反射原理可知P1 , Q,R,P2四點共線,
直線QR的斜率為k= ![]() =
= ![]() ,故直線QR的方程為y=
,故直線QR的方程為y= ![]() (x+a),
(x+a),
由于直線QR過△ABC的重心( ![]() ,
, ![]() ),代入化簡可得3a2﹣4a=0,
),代入化簡可得3a2﹣4a=0,
解得a= ![]() ,或a=0(舍去),故P(
,或a=0(舍去),故P( ![]() ,0),故AP=
,0),故AP= ![]()
故選D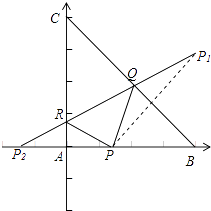
建立坐標系,設點P的坐標,可得P關于直線BC的對稱點P1的坐標,和P關于y軸的對稱點P2的坐標,由P1 , Q,R,P2四點共線可得直線的方程,由于過△ABC的重心,代入可得關于a的方程,解之可得P的坐標,進而可得AP的值.


 巧學巧練系列答案
巧學巧練系列答案科目:高中數學 來源: 題型:
【題目】市環保局舉辦2013年“六五”世界環境日宣傳活動,進行現場抽獎.抽獎規則是:盒中裝有10張大小相同的精美卡片,卡片上分別印有“環保會徽”或“綠色環保標志”圖案.參加者每次從盒中抽取卡片兩張,若抽到兩張都是“綠色環保標志”卡即可獲獎.
(1)活動開始后,一位參加者問:盒中有幾張“綠色環保標志”卡?主持人笑說:我只知道若從盒中抽兩張都不是“綠色環保標志”卡的概率是 ![]() .求抽獎者獲獎的概率;
.求抽獎者獲獎的概率;
(2)現有甲乙丙丁四人依次抽獎,抽后放回,另一人再抽.用ξ表示獲獎的人數.求ξ的分布列及E(ξ),D(ξ).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】解答題
(1)(1)已知命題p:|x2﹣x|≥6,q:x∈Z且“p且q”與“非q”同時為假命題,求x的值.
(2)已知p:x2﹣8x﹣20≤0,q:x2﹣2x+1﹣m2≤0(m>0),若¬p是¬q的必要而不充分條件,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,橢圓C: ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() ,以原點為圓心,橢圓C的短半軸長為半徑的圓與直線x﹣y+2=0相切.
,以原點為圓心,橢圓C的短半軸長為半徑的圓與直線x﹣y+2=0相切. 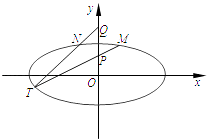
(1)求橢圓C的方程;
(2)已知點P(0,1),Q(0,2).設M,N是橢圓C上關于y軸對稱的不同兩點,直線PM與QN相交于點T,求證:點T在橢圓C上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2015男籃亞錦賽決賽階段,中國男籃以![]() 連勝的不敗成績贏得第
連勝的不敗成績贏得第![]() 屆亞錦賽冠軍,同時拿到亞洲唯一
屆亞錦賽冠軍,同時拿到亞洲唯一![]() 張直通里約奧運會的入場券.賽后,中國男籃主力易建聯榮膺本屆亞錦賽
張直通里約奧運會的入場券.賽后,中國男籃主力易建聯榮膺本屆亞錦賽![]() (最有價值球員),下表是易建聯在這
(最有價值球員),下表是易建聯在這![]() 場比賽中投籃的統計數據.
場比賽中投籃的統計數據.
比分 | 易建聯技術統計 | |||
投籃命中 | 罰球命中 | 全場得分 | 真實得分率 | |
中國 |
|
|
|
|
中國 |
|
|
|
|
中國 |
|
|
|
|
中國 |
|
|
|
|
中國 |
|
|
|
|
中國 |
|
|
|
|
中國 |
|
|
|
|
中國 |
|
|
|
|
中國 |
|
|
|
|
注:(1)表中![]() 表示出手
表示出手![]() 次命中
次命中![]() 次;
次;
(2)![]() (真實得分率)是衡量球員進攻的效率,其計算公式為:
(真實得分率)是衡量球員進攻的效率,其計算公式為:
![]()
(1)從上述![]() 場比賽中隨機選擇一場,求易建聯在該場比賽中
場比賽中隨機選擇一場,求易建聯在該場比賽中![]() 超過
超過![]() 的概率;
的概率;
(2)我們把比分分差不超過![]() 分的比賽稱為“膠著比賽”.為了考驗求易建聯在“膠著比賽”中的發揮情況,從“膠著比賽”中隨機選擇兩場,求易建聯在這兩場比賽中
分的比賽稱為“膠著比賽”.為了考驗求易建聯在“膠著比賽”中的發揮情況,從“膠著比賽”中隨機選擇兩場,求易建聯在這兩場比賽中![]() 至少有一場超過
至少有一場超過![]() 的概率;
的概率;
(3)用![]() 來表示易建聯某場的得分,用
來表示易建聯某場的得分,用![]() 來表示中國隊該場的總分,畫出散點圖如圖所示,請根據散點圖判斷
來表示中國隊該場的總分,畫出散點圖如圖所示,請根據散點圖判斷![]() 與
與![]() 之間是否具有線性相關關系?結合實際簡單說明理由.
之間是否具有線性相關關系?結合實際簡單說明理由.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某保險公司有一款保險產品的歷史收益率(收益率=利潤÷保費收入)的頻率分布直方圖如圖所示:

(Ⅰ)試估計平均收益率;
(Ⅱ)根據經驗,若每份保單的保費在20元的基礎上每增加![]() 元,對應的銷量
元,對應的銷量![]() (萬份)與
(萬份)與![]() (元)有較強線性相關關系,從歷史銷售記錄中抽樣得到如下5組
(元)有較強線性相關關系,從歷史銷售記錄中抽樣得到如下5組![]() 與
與![]() 的對應數據:
的對應數據:

據此計算出的回歸方程為![]() .
.
(i)求參數![]() 的估計值;
的估計值;
(ii)若把回歸方程![]() 當作
當作![]() 與
與![]() 的線性關系,用(Ⅰ)中求出的平均收益率估計此產品的收益率,每份保單的保費定為多少元時此產品可獲得最大收益,并求出該最大收益.
的線性關系,用(Ⅰ)中求出的平均收益率估計此產品的收益率,每份保單的保費定為多少元時此產品可獲得最大收益,并求出該最大收益.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知F1 , F2分別為雙曲線 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左右焦點,如果雙曲線上存在一點P,使得F2關于直線PF1的對稱點恰在y軸上,則該雙曲線的離心率e的取值范圍為( )
=1(a>0,b>0)的左右焦點,如果雙曲線上存在一點P,使得F2關于直線PF1的對稱點恰在y軸上,則該雙曲線的離心率e的取值范圍為( )
A.e> ![]()
B.1<e< ![]()
C.e> ![]()
D.1<e< ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com