【題目】如圖，在△ABC中，角A，B，C所對的邊分別為a，b，c，（ 
a﹣sinC）cosB=sinBcosC，b=4 
． 
（1）求角B的大小；
（2）D為BC邊上一點，若AD=2，S△DAC=2 ，求DC的長．
【答案】
（1）解：∵（ 
a﹣sinC）cosB=sinBcosC，
∴ acosB=sinCcosB+sinBcosC=sin（B+C）=sinA，
在△ABC中，由正弦定理可得： 
，
∴ 
=1，
∴tanB= 
= 
，B∈（0，π），
∴B= 
（2）解：∵S△DAC=2 = 
sin∠DAC，
∴sin∠DAC= 
，
∵0＜∠DAC＜ 
，
∴∠DAC= 
．
在△DAC中，DC2= 
﹣2× 
cos =28．
∴DC=2 
【解析】（1）由（ a﹣sinC）cosB=sinBcosC，利用和差公式、三角形內(nèi)角和定理、誘導公式可得 acosB=sinA，再利用正弦定理、同角三角函數(shù)基本關(guān)系式即可得出．（2）利用三角形面積計算公式、余弦定理即可得出．
【考點精析】關(guān)于本題考查的正弦定理的定義和余弦定理的定義，需要了解正弦定理:
；余弦定理:
;
;
才能得出正確答案．
口算能手系列答案科目：高中數(shù)學 來源： 題型：
【題目】甲乙兩地相距
，貨車從甲地勻速行駛到乙地，速度不得超過
，已知貨車每小時的運輸成本（單位：圓）由可變本和固定組成組成，可變成本是速度平方的
倍，固定成本為
元.
（1）將全程勻速勻速成本
（元）表示為速度
的函數(shù)，并指出這個函數(shù)的定義域；
（2）若
，為了使全程運輸成本最小，貨車應以多大的速度行駛？
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】宜昌市擬在2020年點軍奧體中心落成后申辦2022年湖北省省運會，據(jù)了解，目前武漢，襄陽，黃石等申辦城市因市民擔心賽事費用超支而準備相繼退出，某機構(gòu)為調(diào)查宜昌市市民對申辦省運會的態(tài)度，選了某小區(qū)的100位居民調(diào)查結(jié)果統(tǒng)計如下：
支持 | 不支持 | 合計 | |
年齡不大于50歲 | 80 | ||
年齡大于50歲 | 10 | ||
合計 | 70 | 100 |
（1）根據(jù)已知數(shù)據(jù)，把表格數(shù)據(jù)填寫完整；
（2）能否在犯錯誤的概率不超過
的前提下認為不同年齡與支持申辦省運會無關(guān)？
（3）已知在被調(diào)查的年齡大于50歲的支持者中有5名女性，其中2位是女教師，現(xiàn)從這5名女性中隨機抽取3人，求至多有1位教師的概率．
附：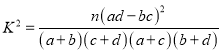 
, 
.
