【題目】在直角坐標系xOy中以O為極點，x軸正半軸為極軸建立坐標系．圓C1 ， 直線C2的極坐標方程分別為ρ=4sinθ，ρcos（ 
）=2 
．
（1）求C1與C2交點的極坐標；
（2）設P為C1的圓心，Q為C1與C2交點連線的中點，已知直線PQ的參數(shù)方程為 
（t∈R為參數(shù)），求a，b的值．
【答案】
（1）解：圓C1，直線C2的直角坐標方程分別為 x2+（y﹣2）2=4，x+y﹣4=0，
解 
得 
或 
，
∴C1與C2交點的極坐標為（4， 
）．（2 
， 
）．
（2）解：由（1）得，P與Q點的坐標分別為（0，2），（1，3），
故直線PQ的直角坐標方程為x﹣y+2=0，
由參數(shù)方程可得y= 
x﹣ 
+1，
∴ 
，
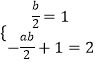解得a=﹣1，b=2．
【解析】（1）先將圓C1 ， 直線C2化成直角坐標方程，再聯(lián)立方程組解出它們交點的直角坐標，最后化成極坐標即可；（2）由（1）得，P與Q點的坐標分別為（0，2），（1，3），從而直線PQ的直角坐標方程為x﹣y+2=0，由參數(shù)方程可得y= x﹣ +1，從而構(gòu)造關于a，b的方程組，解得a，b的值．
閱讀快車系列答案科目：高中數(shù)學 來源： 題型：
【題目】如圖，在直三棱柱ABC﹣A1B1C1中，∠BAC=90°，AB=AC=2，AA1=6，點E、F分別在棱BB1、CC1上，且BE= 
BB1 ， C1F= CC1 ． 
（1）求平面AEF與平面ABC所成角α的余弦值；
（2）若G為BC的中點，A1G與平面AEF交于H，且設 
= 
，求λ的值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，在△ABC中，角A，B，C所對的邊分別為a，b，c，（ 
a﹣sinC）cosB=sinBcosC，b=4 
． 
（1）求角B的大小；
（2）D為BC邊上一點，若AD=2，S△DAC=2 ，求DC的長．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在平面直角坐標系
中，已知點
，直線
，設圓
的半徑為
，且圓心
在直線
上．
（
）若圓心
的坐標為
，過點
作圓
的切線，求切線的方程．
（
）若圓
上存在點
，使
，求圓心
的橫坐標
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】下列說法中不正確的序號為_______．
①若函數(shù)
在
上單調(diào)遞減，則實數(shù)
的取值范圍是
；
②函數(shù)
是偶函數(shù)，但不是奇函數(shù)；
③已知函數(shù)
的定義域為
，則函數(shù)
的定義域是
；
④若函數(shù)
在
上有最小值－4，（，
為非零常數(shù)），則函數(shù)在
上有最大值6．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】選修4﹣5：不等式選講
已知函數(shù)f（x）=|x﹣2|﹣|x﹣5|．
（1）證明：﹣3≤f（x）≤3；
（2）求不等式f（x）≥x2﹣8x+15的解集．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖是一個幾何體的平面展開圖，其中四邊形ABCD為正方形，△PDC, △PBC, △PAB, △PDA為全等的等邊三角形，E、F分別為PA、PD的中點，在此幾何體中，下列結(jié)論中錯誤的為 （ ）
A. 平面BCD⊥平面PAD B. 直線BE與直線AF是異面直線
C. 直線BE與直線CF共面 D. 面PAD與面PBC的交線與BC平行
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
