
【題目】已知函數f(x)=x﹣2sinx.
(Ⅰ)求函數f(x)在 ![]() 上的最值;
上的最值;
(Ⅱ)若存在 ![]() ,使得不等式f(x)<ax成立,求實數a的取值范圍.
,使得不等式f(x)<ax成立,求實數a的取值范圍.
【答案】解:(Ⅰ)f'(x)=1﹣2cosx, ![]()
x |
|
|
|
|
|
|
|
y' | + | 0 | ﹣ | 0 | + | ||
y |
| ↗ | 極大值 | ↘ | 極小值 | ↗ |
|
![]()
(Ⅱ)f(x)<ax,
∴2sinx﹣(1﹣a)x>0
設g(x)=2sinx﹣(1﹣a)x,則g'(x)=2cosx﹣(1﹣a)
由 ![]()
①1﹣a≥2即a≤﹣1,此時g'(x)<0得出g(x)在 ![]() 單調遞減,g(x)<g(0)=0不成立
單調遞減,g(x)<g(0)=0不成立
②1﹣a≤0即a≥1,此時g'(x)>0得出g(x)在 ![]() 單調遞增,g(x)>g(0)=0成立
單調遞增,g(x)>g(0)=0成立
③0<1﹣a<2即﹣1<a<1,令 ![]() ,存在唯一
,存在唯一 ![]() ,使得
,使得 ![]() .當x∈(0,x0)時,g'(x)>0得出g(x)>g(0)=0,
.當x∈(0,x0)時,g'(x)>0得出g(x)>g(0)=0,
∴存在 ![]() ,有g(x)>0成立
,有g(x)>0成立
綜上可知:a>﹣1
【解析】(1)求出導函數,得出極值點,根據極值點求閉區間函數的最值;(2)不等式整理得出2sinx﹣(1﹣a)x>0,構造函數,根據導函數進行分類討論,即最大值大于零即可.


科目:高中數學 來源: 題型:
【題目】為比較甲、乙兩地某月14時的氣溫情況,隨機選取該月中的5天,將這5天中14時的氣溫數據(單位:℃)制成如圖所示的莖葉圖,考慮以下結論:
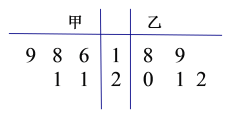
①甲地該月14時的平均氣溫低于乙地該月14時的平均氣溫;
②甲地該月14時的平均氣溫高于乙地該月14時的平均氣溫;
③甲地該月14時的平均氣溫的標準差小于乙地該月14時的平均氣溫的標準差;
④甲地該月14時的平均氣溫的標準差大于乙地該月14時的平均氣溫的標準差,
其中根據莖葉圖能得到的統計結論的編號為( )
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】微信是現代生活進行信息交流的重要工具,據統計,某公司![]() 名員工中
名員工中![]() 的人使用微信,其中每天使用微信時間在一小時以內的有
的人使用微信,其中每天使用微信時間在一小時以內的有![]() 人,其余每天使用微信在一小時以上.若將員工年齡分成青年(年齡小于
人,其余每天使用微信在一小時以上.若將員工年齡分成青年(年齡小于![]() 歲)和中年(年齡不小于
歲)和中年(年齡不小于![]() 歲)兩個階段,使用微信的人中
歲)兩個階段,使用微信的人中![]() 是青年人.若規定:每天使用微信時間在一小時以上為經常使用微信,經常使用微信的員工中
是青年人.若規定:每天使用微信時間在一小時以上為經常使用微信,經常使用微信的員工中![]() 是青年人.
是青年人.
(Ⅰ)若要調查該公司使用微信的員工經常使用微信與年齡的關系,列出![]() 列聯表;
列聯表;
青年人 | 中年人 | 合計 | |
經常使用微信 | |||
不經常使用微信 | |||
合計 |
(Ⅱ)由列聯表中所得數據,是否有![]() 的把握認為“經常使用微信與年齡有關”?
的把握認為“經常使用微信與年齡有關”?
(Ⅲ)采用分層抽樣的方法從“經常使用微信”的人中抽取![]() 人,從這
人,從這![]() 人中任選
人中任選![]() 人,求事件
人,求事件![]() “選出的
“選出的![]() 人均是青年人”的概率.
人均是青年人”的概率.
附:
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國家射擊隊的某隊員射擊一次,命中7~10環的概率如表所示:
命中環數 | 10環 | 9環 | 8環 | 7環 |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求該射擊隊員射擊一次 求:
(1)射中9環或10環的概率;
(2)至少命中8環的概率;(3)命中不足8環的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,BC邊上的高所在直線的方程為x-2y+1=0,∠A的平分線所在的直線方程為y=0.若點B的坐標為(1,2),求點A和點C的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com