
【題目】已知拋物線C: ![]() 的焦點為F,直線
的焦點為F,直線![]() 與y軸的交點為P,與C的交點為Q,且
與y軸的交點為P,與C的交點為Q,且![]() .
.
(1)求C的方程;
(2)過F的直線![]() 與C相交于A,B兩點,若AB的垂直平分線
與C相交于A,B兩點,若AB的垂直平分線![]() 與C相較于M,N兩點,且A,M,B,N四點在同一圓上,求
與C相較于M,N兩點,且A,M,B,N四點在同一圓上,求![]() 的方程.
的方程.
【答案】(1)![]() ;(2)直線
;(2)直線![]() 的方程為
的方程為![]() 或
或![]() .
.
【解析】試題分析:(1)由已知條件,先求![]() 點的坐標,再由
點的坐標,再由![]() 及拋物線的焦半徑公式列方程可求得
及拋物線的焦半徑公式列方程可求得![]() 的值,從而可得拋物線C的方程;(2)由已知條件可知直線
的值,從而可得拋物線C的方程;(2)由已知條件可知直線![]() 與坐標軸不垂直,故可設直線
與坐標軸不垂直,故可設直線![]() 的點參式方程:
的點參式方程: ![]() ,代入
,代入![]() 消元得
消元得![]() .設
.設![]() 由韋達定理及弦長公式表示
由韋達定理及弦長公式表示![]() 的中點
的中點![]() 的坐標及
的坐標及![]() 長,同理可得
長,同理可得![]() 的中點
的中點![]() 的坐標及
的坐標及![]() 的長.由于
的長.由于![]() 垂直平分線
垂直平分線![]() ,故
,故![]() 四點在同一圓上等價于
四點在同一圓上等價于![]() ,由此列方程可求得
,由此列方程可求得![]() 的值,進而可得直線
的值,進而可得直線![]() 的方程.
的方程.
試題解析:(1)設![]() ,代入
,代入![]() ,得
,得![]() .由題設得
.由題設得![]() ,解得
,解得![]() (舍去)或
(舍去)或![]() ,∴C的方程為
,∴C的方程為![]() ;(2)由題設知
;(2)由題設知![]() 與坐標軸不垂直,故可設
與坐標軸不垂直,故可設![]() 的方程為
的方程為![]() ,代入
,代入![]() 得
得![]() .設
.設![]() 則
則![]()
![]() .故
.故![]() 的中點為
的中點為![]() .又
.又![]() 的斜率為
的斜率為![]() 的方程為
的方程為![]() .將上式代入
.將上式代入![]() ,并整理得
,并整理得![]() .設
.設![]() 則
則![]() .故
.故![]() 的中點為
的中點為 .
.
由于![]() 垂直平分線
垂直平分線![]() ,故
,故![]() 四點在同一圓上等價于
四點在同一圓上等價于![]() ,從而
,從而![]() 即
即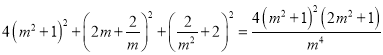 ,化簡得
,化簡得![]() ,解得
,解得![]() 或
或![]() .所求直線
.所求直線![]() 的方程為
的方程為![]() 或
或![]() .
.


 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:高中數學 來源: 題型:
【題目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面上的三個向量,其中
是同一平面上的三個向量,其中 ![]() =(1,2).
=(1,2).
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐標.
的坐標.
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 與2
與2 ![]() ﹣
﹣ ![]() 垂直,求
垂直,求 ![]() 與
與 ![]() 的夾角θ
的夾角θ
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一次測驗共有4個選擇題和2個填空題,每答對一個選擇題得20分,每答對一個填空題得10分,答錯或不答得0分,若某同學答對每個選擇題的概率均為 ![]() ,答對每個填空題的概率均為
,答對每個填空題的概率均為 ![]() ,且每個題答對與否互不影響.
,且每個題答對與否互不影響.
(1)求該同學得80分的概率;
(2)若該同學已經答對了3個選擇題和1個填空題,記他這次測驗的得分為ξ,求ξ的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知空間四邊形ABCD的兩條對角線的長AC=6,BD=8,AC與BD所成的角為30o , E,F,G,H分別是AB,BC,CD,DA的中點,求四邊形EFGH的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCED中,PD⊥面ABCD,四邊形ABCD為平行四邊形,∠DAB=60°,AB=PA=2AD=4, 
(1)若E為PC中點,求證:PA∥平面BDE
(2)求三棱錐D﹣BCP的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位有老年人30人,中年人90人,青年人60人,為了調查他們的身體健康狀況,采用分層抽樣的方法從他們中間抽取一個容量為36的樣本,則應抽取老年人的人數是( )
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 過點
過點![]() ,
, ![]() 為橢圓的半焦距,且
為橢圓的半焦距,且![]() ,過點
,過點![]() 作兩條互相垂直的直線
作兩條互相垂直的直線![]() ,
, ![]() 與橢圓
與橢圓![]() 分別交于另兩點
分別交于另兩點![]() ,
, ![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 的斜率為
的斜率為![]() ,求
,求![]() 的面積;
的面積;
(3)若線段![]() 的中點在
的中點在![]() 軸上,求直線
軸上,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
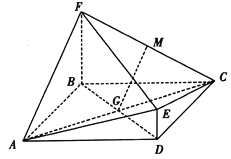
【題目】如圖,菱![]() 與四邊形BDEF相交于BD,
與四邊形BDEF相交于BD, ![]() 平面ABCD,DE//BF,BF=2DE,AF⊥FC,M為CF的中點,
平面ABCD,DE//BF,BF=2DE,AF⊥FC,M為CF的中點, ![]() .
.
(I)求證:GM//平面CDE;
(II)求證:平面ACE⊥平面ACF.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,圓
中,圓![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以O為極點,
為參數),以O為極點, ![]() 軸的非負半軸為極軸建立極坐標系.
軸的非負半軸為極軸建立極坐標系.
(Ⅰ)求圓![]() 的普通方程;
的普通方程;
(Ⅱ)直線![]() 的極坐標方程是
的極坐標方程是![]() ,射線
,射線![]() 與圓C的交點為
與圓C的交點為![]() ,與直線
,與直線![]() 的交點為
的交點為![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com