
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸的極坐標系中,曲線
軸的正半軸為極軸的極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)若![]() ,求直線
,求直線![]() 以及曲線
以及曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的斜率.
的斜率.
【答案】(1)![]() ,
,![]() (2)
(2)![]()
【解析】
(1)根據![]() 的大小消去參數
的大小消去參數![]() ,求得直線
,求得直線![]() 的直角坐標方程,利用極坐標和直角坐標轉化公式,求得曲線
的直角坐標方程,利用極坐標和直角坐標轉化公式,求得曲線![]() 的直角坐標方程.(2)方法1:寫出直線
的直角坐標方程.(2)方法1:寫出直線![]() 的極坐標方程,代入曲線
的極坐標方程,代入曲線![]() 的極坐標方程,根據極坐標系下的弦長公式列方程由此求得直線
的極坐標方程,根據極坐標系下的弦長公式列方程由此求得直線![]() 的斜率.方法2:設出直線的直角坐標方程,聯立直線的方程和曲線
的斜率.方法2:設出直線的直角坐標方程,聯立直線的方程和曲線![]() 的直角坐標方程,利用弦長公式列方程,解方程求得直線斜率.
的直角坐標方程,利用弦長公式列方程,解方程求得直線斜率.
解:(1)由題意,直線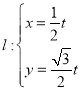 ,可得直線
,可得直線![]() 是過原點的直線,
是過原點的直線,
故其直角坐標方程為![]() ,
,
又![]() ,由
,由![]()
故![]() ;
;
(2)由題意,直線l的極坐標為![]() ,
,
設![]() 、
、![]() 對應的極徑分別為
對應的極徑分別為![]() ,
,![]()
將![]() 代入曲線
代入曲線![]() 的極坐標可得:
的極坐標可得:
![]() ,
,
故![]() ,
,![]() ,
,
![]()
![]()
![]() ,
,
故![]() ,則
,則![]() ,即
,即![]() ,
,![]() ,
,
所以![]() 故直線
故直線![]() 的斜率是
的斜率是![]()
法二:由題意,直線![]() 方程為
方程為![]() ,設
,設![]() 、
、![]() 對應的點坐標為
對應的點坐標為![]()
聯立直線![]() 與曲線
與曲線![]() 的方程
的方程![]() ,消去
,消去![]() 得
得![]() .
.
![]()
![]()
所以![]() ,故直線
,故直線![]() 的斜率是
的斜率是![]() .
.


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案科目:高中數學 來源: 題型:
【題目】已知點![]() 在橢圓
在橢圓![]() 上,過點
上,過點![]() 作
作![]() 軸于點
軸于點![]()
(1)求線段![]() 的中點的軌跡
的中點的軌跡![]() 的方程
的方程
(2)設![]() 、
、![]() 兩點在(1)中軌跡
兩點在(1)中軌跡![]() 上,點
上,點![]() ,兩直線
,兩直線![]() 與
與![]() 的斜率之積為
的斜率之積為![]() ,且(1)中軌跡
,且(1)中軌跡![]() 上存在點
上存在點![]() 滿足
滿足![]() ,當
,當![]() 面積最小時,求直線
面積最小時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() (a>b>0),左、右焦點分別為F1(﹣1,0),F2(1,0),橢圓離心率為
(a>b>0),左、右焦點分別為F1(﹣1,0),F2(1,0),橢圓離心率為![]() ,過點P(4,0)的直線l與橢圓C相交于A、B兩點(A在B的左側).
,過點P(4,0)的直線l與橢圓C相交于A、B兩點(A在B的左側).
(1)求橢圓C的方程;
(2)若B是AP的中點,求直線l的方程;
(3)若B點關于x軸的對稱點是E,證明:直線AE與x軸相交于定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】每年春晚都是萬眾矚目的時刻,這些節目體現的文化內涵、歷史背景等反映了社會的進步.國家的富強,人民生活水平的提高等.某學校高三年級主任開學初為了解學生在看春晚后對節目體現的文化內涵、歷史背景等是否會在今年的高考題中體現進行過思考,特地隨機抽取100名高三學生(其中文科學生50,理科學生50名),進行了調查.統計數據如表所示(不完整):
“思考過” | “沒有思考過” | 總計 | |
文科學生 | 40 | 10 | |
理科學生 | 30 | ||
總計 | 100 |
(1)補充完整所給表格,并根據表格數據計算是否有![]() 的把握認為看春晚后會思考節目體現的文化內涵、歷史背景等與文理科學生有關;
的把握認為看春晚后會思考節目體現的文化內涵、歷史背景等與文理科學生有關;
(2)①現從上表的”思考過”的文理科學生中按分層抽樣選出7人.再從這7人中隨機抽取4人,記這4人中“文科學生”的人數為![]() ,試求
,試求![]() 的分布列與數學期望;
的分布列與數學期望;
②現設計一份試卷(題目知識點來自春晚相關知識整合與變化),假設“思考過”的學生及格率為![]() ,“沒有思考過”的學生的及格率為
,“沒有思考過”的學生的及格率為![]() .現從“思考過”與“沒有思考過”的學生中分別隨機抽取一名學生進行測試,求兩人至少有一個及格的概率.
.現從“思考過”與“沒有思考過”的學生中分別隨機抽取一名學生進行測試,求兩人至少有一個及格的概率.
附參考公式: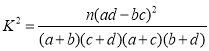 ,其中
,其中![]() .
.
參考數據:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() 在
在![]() 上有定義,實數
上有定義,實數![]() 和
和![]() 滿足
滿足![]() ,若
,若![]() 在區間
在區間![]() 上不存在最小值,則稱
上不存在最小值,則稱![]() 在
在![]() 上具有性質
上具有性質![]() .
.
(1)當![]() ,且
,且![]() 在區間
在區間![]() 上具有性質
上具有性質![]() 時,求常數
時,求常數![]() 的取值范圍;
的取值范圍;
(2)已知![]() (
(![]() ),且當
),且當![]() 時,
時,![]() ,判別
,判別![]() 在區間
在區間![]() 上是否具有性質
上是否具有性質![]() ,試說明理由.
,試說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com