
【題目】每年春晚都是萬眾矚目的時刻,這些節目體現的文化內涵、歷史背景等反映了社會的進步.國家的富強,人民生活水平的提高等.某學校高三年級主任開學初為了解學生在看春晚后對節目體現的文化內涵、歷史背景等是否會在今年的高考題中體現進行過思考,特地隨機抽取100名高三學生(其中文科學生50,理科學生50名),進行了調查.統計數據如表所示(不完整):
“思考過” | “沒有思考過” | 總計 | |
文科學生 | 40 | 10 | |
理科學生 | 30 | ||
總計 | 100 |
(1)補充完整所給表格,并根據表格數據計算是否有![]() 的把握認為看春晚后會思考節目體現的文化內涵、歷史背景等與文理科學生有關;
的把握認為看春晚后會思考節目體現的文化內涵、歷史背景等與文理科學生有關;
(2)①現從上表的”思考過”的文理科學生中按分層抽樣選出7人.再從這7人中隨機抽取4人,記這4人中“文科學生”的人數為![]() ,試求
,試求![]() 的分布列與數學期望;
的分布列與數學期望;
②現設計一份試卷(題目知識點來自春晚相關知識整合與變化),假設“思考過”的學生及格率為![]() ,“沒有思考過”的學生的及格率為
,“沒有思考過”的學生的及格率為![]() .現從“思考過”與“沒有思考過”的學生中分別隨機抽取一名學生進行測試,求兩人至少有一個及格的概率.
.現從“思考過”與“沒有思考過”的學生中分別隨機抽取一名學生進行測試,求兩人至少有一個及格的概率.
附參考公式: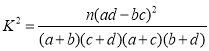 ,其中
,其中![]() .
.
參考數據:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【答案】(1)列聯表見解析,有;(2)①見解析;②![]() .
.
【解析】
(1)根據題意,得出![]() 的列聯表,利用公式求的
的列聯表,利用公式求的![]() 的值,即可得出結論;
的值,即可得出結論;
(2)①由題意,得出所以![]() 的所有可能取值為
的所有可能取值為![]() ,取得隨機變量取每個值對應的概率,得出分布列,利用期望的公式,即可求解.
,取得隨機變量取每個值對應的概率,得出分布列,利用期望的公式,即可求解.
②設“思考過”的學生的及格率![]() ;“沒有思考過”的學生的及格率
;“沒有思考過”的學生的及格率![]() ,根據獨立事件的概率計算公式,即可求解.
,根據獨立事件的概率計算公式,即可求解.
(1)填表如下:
“思考過” | “沒有思考過” | 總計 | |
文科學生 | 40 | 10 | 50 |
理科學生 | 30 | 20 | 50 |
總計 | 70 | 30 | 100 |
由上表得,![]() 的觀測值
的觀測值![]() ,
,
故有![]() 的把握認為看春晚節目后是否會思考與文理科學生有關.
的把握認為看春晚節目后是否會思考與文理科學生有關.
(2)①由題意,得抽取的100名學生中“思考過”的有文科學生40人,理科學生30人,所以抽取7人中文科學生有4人,理科學生有3人,所以![]() 的所有可能取值為1,2,3,4.
的所有可能取值為1,2,3,4.
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
所以![]() 的分布列為
的分布列為
| 1 | 2 | 3 | 4 |
P |
|
|
|
|
故數學期望為![]() .
.
②設“思考過”的學生的及格率為![]() ,則
,則![]() ;“沒有思考過”的學生的及格率為
;“沒有思考過”的學生的及格率為![]() ,則
,則![]() ,所以兩人至少有一個及格的概率為
,所以兩人至少有一個及格的概率為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,天花板上掛著3串玻璃球,射擊玻璃球規則:每次擊中1球,每串中下面球沒擊中,上面球不能擊中,則把這6個球全部擊中射擊方法數是( )
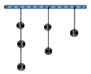
A.78B.60C.48D.36
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某生物小組為了研究溫度對某種酶的活性的影響進行了一組實驗,得到的實驗數據經整理得到如下的折線圖:
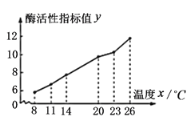
(1)由圖可以看出,這種酶的活性![]() 與溫度
與溫度![]() 具有較強的線性相關性,請用相關系數加以說明;
具有較強的線性相關性,請用相關系數加以說明;
(2)求![]() 關于
關于![]() 的線性回歸方程,并預測當溫度為
的線性回歸方程,并預測當溫度為![]() 時,這種酶的活性指標值.(計算結果精確到0.01)
時,這種酶的活性指標值.(計算結果精確到0.01)
參考數據:![]() ,
,![]() ,
,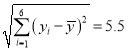 ,
,![]() .
.
參考公式:相關系數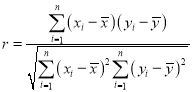 .
.
回歸直線方程![]() ,
,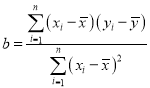 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列有關線性回歸分析的四個命題:
①線性回歸直線必過樣本數據的中心點(![]() );
);
②回歸直線就是散點圖中經過樣本數據點最多的那條直線;
③當相關性系數![]() 時,兩個變量正相關;
時,兩個變量正相關;
④如果兩個變量的相關性越強,則相關性系數![]() 就越接近于
就越接近于![]() .
.
其中真命題的個數為( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知球![]() 是正三棱錐(底面為正三角形,頂點在底面的射影為底面中心)
是正三棱錐(底面為正三角形,頂點在底面的射影為底面中心)![]() 的外接球,
的外接球,![]() ,
,![]() ,點
,點![]() 在線段
在線段![]() 上,且
上,且![]() ,過點
,過點![]() 作球
作球![]() 的截面,則所得截面圓面積的取值范圍是( )
的截面,則所得截面圓面積的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體ABCD﹣A1B1C1D1的棱長為a,線段B1D1上有兩個動點E,F,且EF![]() a,以下結論正確的有( )
a,以下結論正確的有( )

A.AC⊥BE
B.點A到△BEF的距離為定值
C.三棱錐A﹣BEF的體積是正方體ABCD﹣A1B1C1D1體積的![]()
D.異面直線AE,BF所成的角為定值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在幾何體ABCDE中,四邊形ABCD是矩形,AB![]() 平面BEC,BE
平面BEC,BE![]() EC,AB=BE=EC=2,G,F分別是線段BE,DC的中點.
EC,AB=BE=EC=2,G,F分別是線段BE,DC的中點.
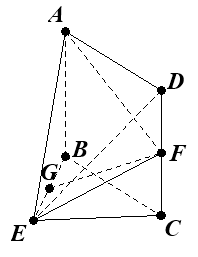
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求平面AEF與平面BEC所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某社區消費者協會為了解本社區居民網購消費情況,隨機抽取了100位居民作為樣本,就最近一年來網購消費金額(單位:千元),網購次數和支付方式等進行了問卷調查.經統計這100位居民的網購消費金額均在區間![]() 內,按
內,按![]() 分成6組,其頻率分布直方圖如圖所示.
分成6組,其頻率分布直方圖如圖所示.
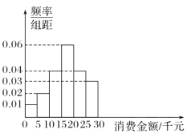
(1)估計該社區居民最近一年來網購消費金額的中位數;
(2)將網購消費金額在20千元以上者稱為“網購迷”,補全下面的![]() 列聯表,并判斷有多大把握認為“網購迷與性別有關系”
列聯表,并判斷有多大把握認為“網購迷與性別有關系”
男 | 女 | 總計 | |
網購迷 | 20 | ||
非網購迷 | 45 | ||
總計 | 100 |
附:![]() .
.
臨界值表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com