
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,點
,點![]() 在
在![]() 上.
上.
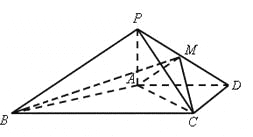
(1)求證:![]() ;
;
(2)若二面角![]() 的大小為
的大小為![]() ,求
,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)詳見解析;(2)![]()
【解析】
試題第一問應用空間的垂直關系的轉(zhuǎn)換,應用線面垂直得出線線垂直的
關系,第二問根據(jù)所給的二面角的大小,結(jié)合空間向量,從而確定出
點![]() 的位置,再用空間向量確定出線面角的正弦值.
的位置,再用空間向量確定出線面角的正弦值.
試題解析:(Ⅰ)如圖,設![]() 為
為![]() 的中點,連結(jié)
的中點,連結(jié)![]() ,則
,則![]() ,所以四邊形
,所以四邊形![]() 為平行四邊形,
為平行四邊形,
故![]() ,又
,又![]() ,
,
所以![]() ,故
,故![]() ,
,
又因為![]() 平面
平面![]() ,所以
,所以![]() ,
,
且![]() ,所以
,所以![]() 平面
平面![]() ,故有
,故有![]()
![]() 分
分
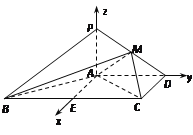
(Ⅱ)如圖,以![]() 為原點,分別以射線
為原點,分別以射線![]() 為
為![]() 軸的正半軸,建立空間直角坐標系
軸的正半軸,建立空間直角坐標系![]() .
.
則![]() ,
,
設![]() ,易得
,易得![]() ,
,
設平面![]() 的一個法向量為
的一個法向量為![]() ,則
,則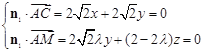 ,
,
令![]() 得
得![]() ,即
,即![]() .
.
又平面![]() 的一個法向量為
的一個法向量為![]() ,
,
由題知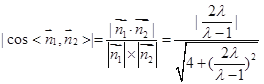
![]() ,解得
,解得![]() ,
,
即![]() ,而
,而![]() 是平面
是平面![]() 的一個法向量,
的一個法向量,
設平面![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,則
,則![]() .
.
故直線![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]() .
.![]() 分
分


 鴻圖圖書寒假作業(yè)假期作業(yè)吉林大學出版社系列答案
鴻圖圖書寒假作業(yè)假期作業(yè)吉林大學出版社系列答案科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
已知曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以直角坐標系的原點
為參數(shù)),以直角坐標系的原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸,建立極坐標系,直線
軸的正半軸為極軸,建立極坐標系,直線![]() 的極坐標方程是:
的極坐標方程是:![]()
(1)求曲線![]() 的普通方程和直線
的普通方程和直線![]() 的直角坐標方程.
的直角坐標方程.
(2)點![]() 是曲線
是曲線![]() 上的動點,求點
上的動點,求點![]() 到直線
到直線![]() 距離的最大值與最小值.
距離的最大值與最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以坐標原點
為參數(shù)),以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸的極坐標系中,曲線
軸的正半軸為極軸的極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)若![]() ,求直線
,求直線![]() 以及曲線
以及曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】我國南宋數(shù)學家楊輝在所著的《詳解九章算法》一書中用如圖所示的三角形解釋二項展開式的系數(shù)規(guī)律,現(xiàn)把楊輝三角中的數(shù)從上到下,從左到右依次排列,得數(shù)列:1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,…,記作數(shù)列![]() ,若數(shù)列
,若數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,則
,則![]() _____.
_____.

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]()
(1)若曲線![]() 在x=1處的切線為y=2x-3,求實教a,b的值.
在x=1處的切線為y=2x-3,求實教a,b的值.
(2)若a=0,且![]() -2對一切正實數(shù)x值成立,求實數(shù)b的取值范圍.
-2對一切正實數(shù)x值成立,求實數(shù)b的取值范圍.
(3)若b=4,求函數(shù)![]() 的單調(diào)區(qū)間.
的單調(diào)區(qū)間.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如表中數(shù)表為“森德拉姆篩”,其特點是每行每列都成等差數(shù)列,記第i行,第j列的數(shù)為aij,則數(shù)字41在表中出現(xiàn)的次數(shù)為( )
2 | 3 | 4 | 5 | 6 | 7 | … |
3 | 5 | 7 | 9 | 11 | 13 | … |
4 | 7 | 10 | 13 | 16 | 19 | … |
5 | 9 | 13 | 17 | 21 | 25 | … |
6 | 11 | 16 | 21 | 26 | 31 | … |
7 | 13 | 19 | 25 | 31 | 37 | … |
… | … | … | … | … | … | … |
A.4B.8C.9D.12
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù) ,函數(shù)F(x)=f(x)﹣b有四個不同的零點x1,x2,x3,x4,且滿足:x1<x2<x3<x4,則
,函數(shù)F(x)=f(x)﹣b有四個不同的零點x1,x2,x3,x4,且滿足:x1<x2<x3<x4,則![]() 的取值范圍是( )
的取值范圍是( )
A.[![]() ,+∞)B.(3,
,+∞)B.(3,![]() ]C.[3,+∞)D.
]C.[3,+∞)D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知拋物線![]() (
(![]() ),過點
),過點![]() (
(![]() )的直線
)的直線![]() 與
與![]() 交于
交于![]() 、
、![]() 兩點.
兩點.
(1)若![]() ,求證:
,求證:![]() 是定值(
是定值(![]() 是坐標原點);
是坐標原點);
(2)若![]() (
(![]() 是確定的常數(shù)),求證:直線
是確定的常數(shù)),求證:直線![]() 過定點,并求出此定點坐標;
過定點,并求出此定點坐標;
(3)若![]() 的斜率為1,且
的斜率為1,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com