【題目】
已知函數
，且
。
（I）試用含
的代數式表示
；
（Ⅱ）求
的單調區間；
（Ⅲ）令
，設函數在
處取得極值，記點
，證明：線段
與曲線存在異于
、
的公共點。
【答案】（I）
（Ⅱ）當
時，函數
的單調增區間為
和
，單調減區間為
；
當
時，函數的單調增區間為R；
當
時，函數的單調增區間為
和
，單調減區間為
。
（Ⅲ）證明見解析。
【解析】
試題（Ⅰ）從導數出發，利用
即得
與
的關系式：（Ⅱ）求函數單調區間，關鍵研究導函數零點分布情況：因為導函數有兩個零點：
，
，因此需分三種情況進行討論，此時最容易遺漏相等的情況（Ⅲ）先根據極值求出
、
的坐標
，再聯立方程確定線段MN與曲線
的交點，由
易得
，因此線段
與曲線存在異于、的公共點
試題解析：解：（Ⅰ）依題意得
，由
得…2分
（Ⅱ）由（Ⅰ）得
，
故
，令
，則或
①當時，
，當
變化時，
的變化情況如下表
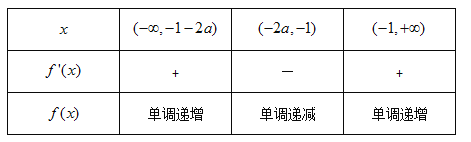
可得函數的單調增區間為
和，單調減區間為
。
②當時，
，此時
恒成立，且僅在處，故函數的單調增區間為
；
③當時，
，函數的單調增區間為和，單調減區間為
（Ⅲ）當
時，
，
，
。
由（Ⅱ）得的單調增區間為和
，單調減區間為
，
函數在處取得極值，故
直線的方程為
由
得
令
，易得
的圖像在
內是一條連續不斷的曲線，
故在內存在零點
，這表明線段與曲線有異于
的公共點
科目：高中數學 來源： 題型：
【題目】選修4-4：極坐標與參數方程
在極坐標系下，已知圓O：
和直線
（1）求圓O和直線l的直角坐標方程；
（2）當
時，求直線l與圓O公共點的一個極坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，其中
．
（1）若函數
在點
處的切線方程為
，求
的值；
（2）若函數有兩個極值點
，證明：
成等差數列；
（3）若函數有三個零點
，對任意的
，不等式
恒成立，求
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
已知曲線
的參數方程為
（
為參數），以直角坐標系的原點
為極點，
軸的正半軸為極軸，建立極坐標系，直線
的極坐標方程是：
（1）求曲線的普通方程和直線的直角坐標方程.
（2）點
是曲線上的動點，求點到直線距離的最大值與最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某快遞公司收取快遞費用的標準是：重量不超過
的包裹收費
元；重量超過
的包裹，除
收費
元之外，超過
的部分，每超出
（不足
，按
計算）需再收
元.該公司將最近承攬的
件包裹的重量統計如下：
包裹重量（單位： |
|
|
|
|
|
包裹件數 |
|
|
|
|
|
公司對近
天，每天攬件數量統計如下表：
包裹件數范圍 |
|
|
|
|
|
包裹件數 （近似處理） |
|
|
|
|
|
天數 |
|
|
|
|
|
以上數據已做近似處理，并將頻率視為概率.
（1）計算該公司未來
天內恰有
天攬件數在
之間的概率；
（2）（i）估計該公司對每件包裹收取的快遞費的平均值；
（ii）公司將快遞費的三分之一作為前臺工作人員的工資和公司利潤，剩余的用作其他費用.目前前臺有工作人員
人，每人每天攬件不超過
件，工資
元.公司正在考慮是否將前臺工作人員裁減
人，試計算裁員前后公司每日利潤的數學期望，并判斷裁員是否對提高公司利潤更有利？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，曲線
的參數方程為
為參數且
，
，
，曲線
的參數方程為
為參數），以
為極點，
軸正半軸為極軸建立極坐標系，曲線
的極坐標方程為
．
（1）求的普通方程及的直角坐標方程；
（2）若曲線與曲線
分別交于點
，
，求
的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，直線
的參數方程為
（
為參數），以坐標原點
為極點，
軸的正半軸為極軸的極坐標系中，曲線
的極坐標方程為
.
（1）若
，求直線以及曲線的直角坐標方程；
（2）若直線與曲線交于
兩點，且
，求直線的斜率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，函數F（x）＝f（x）﹣b有四個不同的零點x1，x2，x3，x4，且滿足：x1＜x2＜x3＜x4，則
的取值范圍是（ ）
A.[
，+∞）B.（3，
]C.[3，+∞）D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
