
【題目】已知拋物線![]() 和圓
和圓![]() ,傾斜角為45°的直線
,傾斜角為45°的直線![]() 過拋物線
過拋物線![]() 的焦點,且
的焦點,且![]() 與圓
與圓![]() 相切.
相切.
(1)求![]() 的值;
的值;
(2)動點![]() 在拋物線
在拋物線![]() 的準線上,動點
的準線上,動點![]() 在
在![]() 上,若
上,若![]() 在
在![]() 點處的切線
點處的切線![]() 交
交![]() 軸于點
軸于點![]() ,設(shè)
,設(shè)![]() .求證點
.求證點![]() 在定直線上,并求該定直線的方程.
在定直線上,并求該定直線的方程.
 陽光同學一線名師全優(yōu)好卷系列答案
陽光同學一線名師全優(yōu)好卷系列答案科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() 與曲線
與曲線![]() ,(
,(![]() 為參數(shù)).以坐標原點為極點,
為參數(shù)).以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)寫出曲線![]() ,
,![]() 的極坐標方程;
的極坐標方程;
(2)在極坐標系中,已知![]() 與
與![]() ,
,![]() 的公共點分別為
的公共點分別為![]() ,
,![]() ,
,![]() ,當
,當![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,其焦距為
,其焦距為![]() ,點E為橢圓的上頂點,且
,點E為橢圓的上頂點,且![]() .
.
(1)求橢圓C的方程;
(2)設(shè)圓![]() 的切線l交橢圓C于A,B兩點(O為坐標原點),求證
的切線l交橢圓C于A,B兩點(O為坐標原點),求證![]() ;
;
(3)在(2)的條件下,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列說法:
①分類變量![]() 與
與![]() 的隨機變量
的隨機變量![]() 越大,說明“
越大,說明“![]() 與
與![]() 有關(guān)系”的可信度越大;
有關(guān)系”的可信度越大;
②以模型![]() 去擬合一組數(shù)據(jù)時,為了求出回歸方程,設(shè)
去擬合一組數(shù)據(jù)時,為了求出回歸方程,設(shè)![]() ,將其變換后得到線性方程
,將其變換后得到線性方程![]() ,則
,則![]() ,
,![]() 的值分別是
的值分別是![]() 和
和![]() ;
;
③在殘差圖中,殘差點分布的帶狀區(qū)域的寬度越狹窄,其模型擬合的精度越高;
④若變量![]() 和
和![]() 滿足關(guān)系
滿足關(guān)系![]() ,且變量
,且變量![]() 與
與![]() 正相關(guān),則
正相關(guān),則![]() 與
與![]() 也正相關(guān).
也正相關(guān).
正確的個數(shù)是________.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為了迎接2019年全國文明城市評比,某市文明辦對市民進行了一次文明創(chuàng)建知識的網(wǎng)絡(luò)問卷調(diào)查.每一位市民有且僅有一次參加機會,通過隨機抽樣,得到參加問卷調(diào)查的1000人的得分(滿分:100分)數(shù)據(jù),統(tǒng)計結(jié)果如下表所示:
組別 |
|
|
|
|
|
|
|
頻數(shù) | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由頻數(shù)分布表可以認為,此次問卷調(diào)查的得分![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,
,![]() 近似為這1000人得分的平均值(同一組數(shù)據(jù)用該組區(qū)間的中點值作為代表),請利用正態(tài)分布的知識求
近似為這1000人得分的平均值(同一組數(shù)據(jù)用該組區(qū)間的中點值作為代表),請利用正態(tài)分布的知識求![]() ;
;
(2)在(1)的條件下,文明辦為此次參加問卷調(diào)查的市民制定如下獎勵方案:
(i)得分不低于![]() 的可以獲贈2次隨機話費,得分低于
的可以獲贈2次隨機話費,得分低于![]() 的可以獲贈1次隨機話費;
的可以獲贈1次隨機話費;
(ii)每次獲贈的隨機話費和對應(yīng)的概率為:
獲贈的隨機話費(單位:元) | 20 | 40 |
概率 |
|
|
現(xiàn)市民小王要參加此次問卷調(diào)查,記![]() (單位:元)為該市民參加問卷調(diào)查獲贈的話費,求
(單位:元)為該市民參加問卷調(diào)查獲贈的話費,求![]() 的分布列及數(shù)學期望.
的分布列及數(shù)學期望.
附:①![]() ;
;
②若![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在極坐標系中,過曲線![]() 外的一點
外的一點![]() (其中
(其中![]() ,
,![]() 為銳角)作平行于
為銳角)作平行于![]() 的直線
的直線![]() 與曲線分別交于
與曲線分別交于![]() .
.
(Ⅰ) 寫出曲線![]() 和直線
和直線![]() 的普通方程(以極點為原點,極軸為
的普通方程(以極點為原點,極軸為![]() 軸的正半軸建系);
軸的正半軸建系);
(Ⅱ)若![]() 成等比數(shù)列,求
成等比數(shù)列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】春節(jié)期間爆發(fā)的新型冠狀病毒(COVID-19)是新中國成立以來感染人數(shù)最多的一次疫情.一個不知道自己已感染但處于潛伏期的甲從疫區(qū)回到某市過春節(jié),回到家鄉(xiāng)后與朋友乙、丙、丁相聚過,最終乙、丙、丁也感染了新冠病毒.可以肯定的是乙受甲感染的,丙是受甲或乙感染的,假設(shè)他受甲和受乙感染的概率分別是![]() 和
和![]() .丁是受甲、乙或丙感染的,假設(shè)他受甲、乙和丙感染的概率分別是
.丁是受甲、乙或丙感染的,假設(shè)他受甲、乙和丙感染的概率分別是![]() 、
、![]() 和
和![]() .在這種假設(shè)之下,乙、丙、丁中直接受甲感染的人數(shù)為
.在這種假設(shè)之下,乙、丙、丁中直接受甲感染的人數(shù)為![]() .
.
(1)求![]() 的分布列和數(shù)學期望;
的分布列和數(shù)學期望;
(2)該市在發(fā)現(xiàn)在本地出現(xiàn)新冠病毒感染者后,迅速采取應(yīng)急措施,其中一項措施是各區(qū)必須每天及時,上報新增疑似病例人數(shù).![]() 區(qū)上報的連續(xù)
區(qū)上報的連續(xù)![]() 天新增疑似病例數(shù)據(jù)是“總體均值為
天新增疑似病例數(shù)據(jù)是“總體均值為![]() ,中位數(shù)
,中位數(shù)![]() ”,
”,![]() 區(qū)上報的連續(xù)
區(qū)上報的連續(xù)![]() 天新增疑似病例數(shù)據(jù)是“總體均值為
天新增疑似病例數(shù)據(jù)是“總體均值為![]() ,總體方差為
,總體方差為![]() ”.設(shè)
”.設(shè)![]() 區(qū)和
區(qū)和![]() 區(qū)連續(xù)
區(qū)連續(xù)![]() 天上報新增疑似病例人數(shù)分別為
天上報新增疑似病例人數(shù)分別為![]() 和
和![]() ,
,![]() 和
和![]() 分別表示
分別表示![]() 區(qū)和
區(qū)和![]() 區(qū)第
區(qū)第![]() 天上報新增疑似病例人數(shù)(
天上報新增疑似病例人數(shù)(![]() 和
和![]() 均為非負).記
均為非負).記![]() ,
,![]() .
.
①試比較![]() 和
和![]() 的大小;
的大小;
②求![]() 和
和![]() 中較小的那個字母所對應(yīng)的
中較小的那個字母所對應(yīng)的![]() 個數(shù)有多少組?
個數(shù)有多少組?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,其中
,其中![]() .
.
(I)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若![]() R上有兩個不同的零點
R上有兩個不同的零點![]()
![]() ,且
,且![]() ,求實數(shù)a的取值范圍.
,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)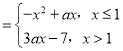 ,若存在x1,x2∈R且x1≠x2,使得f(x1)=f(x2)成立,則實數(shù)a的取值范圍是( )
,若存在x1,x2∈R且x1≠x2,使得f(x1)=f(x2)成立,則實數(shù)a的取值范圍是( )
A.[3,+∞)B.(3,+∞)C.(﹣∞,3)D.(﹣∞,3]
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com