
【題目】已知函數![]() ,其中
,其中![]() .
.
(I)求![]() 的單調區間;
的單調區間;
(Ⅱ)若![]() R上有兩個不同的零點
R上有兩個不同的零點![]()
![]() ,且
,且![]() ,求實數a的取值范圍.
,求實數a的取值范圍.
【答案】(I)見解析(Ⅱ)![]() .
.
【解析】
(I)求導得![]() ,討論
,討論![]() 和
和![]() 即可解得單調區間;
即可解得單調區間;
(Ⅱ)要使得![]() R上有兩個不同的零點
R上有兩個不同的零點![]()
![]() ,且
,且![]() ,由(I)可知
,由(I)可知![]() 取得極小值,極小值小于0,可解得
取得極小值,極小值小于0,可解得![]() .借助引理1:
.借助引理1:![]()
![]() ;引理2:
;引理2:![]()
![]() 證明
證明![]() 存在
存在![]() ,使
,使![]() .
.![]() ,使
,使![]() .即證得
.即證得![]() 符合題意.
符合題意.
(I)![]() .
.
當![]() 時,
時,![]() ,
,![]() 在R上單調遞減;
在R上單調遞減;
當![]() 時,由
時,由![]() 解得
解得![]() ,
,
當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() ,
,
所以![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
綜上,![]() 時,
時,![]() 在R上單調遞減;
在R上單調遞減;
![]() 時
時![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
(Ⅱ)引理1:![]()
![]() .
.
證明:令![]() ,
,
則![]() ,
,![]() ,
,
![]() 在
在![]() 上單調遞增,又
上單調遞增,又![]() ,
,
![]() .
.![]() 在
在![]() 上單調遞增,
上單調遞增,
又![]() ,
,![]() .
.
引理2:![]()
![]() .
.
證明:![]() .
.
令![]()
![]() ,
,
則![]() ,
,![]() 在
在![]() 上單調遞減.
上單調遞減.
![]() ,故得證.
,故得證.
下求實數![]() 的取值范圍.由(1)知要使
的取值范圍.由(1)知要使![]() 有兩個零點,
有兩個零點,![]() ,
,
此時,![]() .
.
令![]() ,解得
,解得![]() .
.
又![]() ,
,![]() ,使
,使![]() .
.
由引理1和引理2知:
![]() ,
,![]() .
.
使![]()
![]()
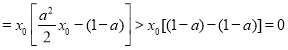 .
.
![]() ,使
,使![]() .
.
綜上:![]() .
.


科目:高中數學 來源: 題型:
【題目】已知,圖中直棱柱![]() 的底面是菱形,其中
的底面是菱形,其中![]() .又點
.又點![]() 分別在棱
分別在棱![]() 上運動,且滿足:
上運動,且滿足:![]() ,
,![]() .
.
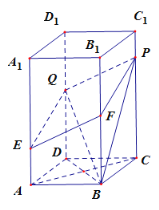
(1)求證:![]() 四點共面,并證明
四點共面,并證明![]() ∥平面
∥平面![]() .
.
(2)是否存在點![]() 使得二面角
使得二面角![]() 的余弦值為
的余弦值為![]() ?如果存在,求出
?如果存在,求出![]() 的長;如果不存在,請說明理由.
的長;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 和圓
和圓![]() ,傾斜角為45°的直線
,傾斜角為45°的直線![]() 過拋物線
過拋物線![]() 的焦點,且
的焦點,且![]() 與圓
與圓![]() 相切.
相切.
(1)求![]() 的值;
的值;
(2)動點![]() 在拋物線
在拋物線![]() 的準線上,動點
的準線上,動點![]() 在
在![]() 上,若
上,若![]() 在
在![]() 點處的切線
點處的切線![]() 交
交![]() 軸于點
軸于點![]() ,設
,設![]() .求證點
.求證點![]() 在定直線上,并求該定直線的方程.
在定直線上,并求該定直線的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了了解學生對《3.12植樹節》活動節日的相關內容,學校進行了一次10道題的問卷調查,從該校學生中隨機抽取50人,統計了每人答對的題數,將統計結果分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五組,得到如下頻率分布直方圖.
五組,得到如下頻率分布直方圖.
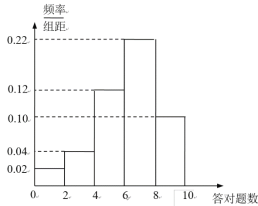
(1)若答對一題得10分,答錯和未答不得分,估計這50名學生成績的平均分;
(2)若從答對題數在![]() 內的學生中隨機抽取2人,求恰有1人答對題數在
內的學生中隨機抽取2人,求恰有1人答對題數在![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】四棱錐S-ABCD中,底面ABCD是邊長為2的菱形,![]() ,
,![]() ,二面角S-BD-C的余弦值為
,二面角S-BD-C的余弦值為![]() .
.
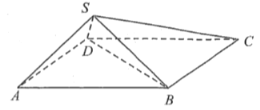
(I)證明:平面![]() 平面SBD;
平面SBD;
(Ⅱ)求二面角A-SD-C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(I)當a=-1時,
①求曲線y= f(x)在點(0,f(0))處的切線方程;
②求函數f(x)的最小值;
(II)求證:當![]() 時,曲線
時,曲線![]() 與
與![]() 有且只有一個交點.
有且只有一個交點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l的參數方程為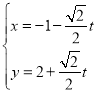 (t為參數),以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C1的極坐標方程為
(t為參數),以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C1的極坐標方程為![]() ,曲線C2的直角坐標方程為
,曲線C2的直角坐標方程為![]() .
.
(1)若直線l與曲線C1交于M、N兩點,求線段MN的長度;
(2)若直線l與x軸,y軸分別交于A、B兩點,點P在曲線C2上,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐P-ABCD,四邊形ABCD是邊長為3的正方形,平面![]() 平面
平面![]() ,
,![]() 于點O,
于點O,![]() ,點E在棱PB上,
,點E在棱PB上,![]() .
.
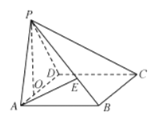
(1)當![]() 時,求直線AE與平面PCD所成角的正弦值;
時,求直線AE與平面PCD所成角的正弦值;
(2)若二面角B-PC-D的余弦值為![]() ,求PO的長.
,求PO的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com