
【題目】已知函數![]() 的定義域為
的定義域為![]() ,值域為
,值域為![]() ,即
,即![]() ,若
,若![]() ,則稱
,則稱![]() 在
在![]() 上封閉.
上封閉.
(1)分別判斷函數![]() ,
, ![]() 在
在![]() 上是否封閉,說明理由;
上是否封閉,說明理由;
(2)函數![]() 的定義域為
的定義域為![]() ,且存在反函數
,且存在反函數![]() ,若函數
,若函數![]() 在
在![]() 上封閉,且函數
上封閉,且函數![]() 在
在![]() 上也封閉,求實數
上也封閉,求實數![]() 的取值范圍;
的取值范圍;
(3)已知函數![]() 的定義域為
的定義域為![]() ,對任意
,對任意![]() ,若
,若![]() ,有
,有![]() 恒成立,則稱
恒成立,則稱![]() 在
在![]() 上是單射,已知函數
上是單射,已知函數![]() 在
在![]() 上封閉且單射,并且滿足
上封閉且單射,并且滿足![]()
![]() ,其中
,其中![]() (
(![]() ),
),![]() ,證明:存在
,證明:存在![]() 的真子集,
的真子集, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,使得
,使得![]() 在所有
在所有![]() (
(![]() )上封閉.
)上封閉.
【答案】(1)見解析;(2)![]() ;(3)見解析.
;(3)見解析.
【解析】試題分析:(1)根據![]() 在
在![]() 上封閉的定義,分別求出函數
上封閉的定義,分別求出函數![]() ,
, ![]() 在
在![]() 上的值域,即可判斷是否封閉;(2)函數
上的值域,即可判斷是否封閉;(2)函數![]() 在D上封閉,則
在D上封閉,則![]() .函數
.函數![]() 在
在![]() 上封閉,則
上封閉,則![]() ,得到:
,得到: ![]() .從而問題轉化為:
.從而問題轉化為: ![]() 在
在![]() 兩不等實根.(3)分兩種情況:
兩不等實根.(3)分兩種情況: ![]() 和
和![]() ,第一種情況顯然不成立,第二種情況,因為
,第一種情況顯然不成立,第二種情況,因為![]() 是單射,因此取一個
是單射,因此取一個![]() ,則
,則![]() 是唯一的使得
是唯一的使得![]() 的根,換句話說
的根,換句話說![]() 考慮到
考慮到![]() ,即
,即![]() ,因為
,因為![]() 是單射,則
是單射,則![]() 這樣就有了
這樣就有了![]() .接著令
.接著令![]() ,并重復上述論證證明
,并重復上述論證證明![]() ..
..
試題解析:
(1)因為函數![]() 的定義域為
的定義域為![]() ,值域為
,值域為![]() ,(取一個具體例子也可),
,(取一個具體例子也可),
所以![]() 在
在![]() 上不封閉.
上不封閉.
![]()
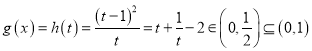
![]() 在
在![]() 上封閉
上封閉
(2)函數![]() 在D上封閉,則
在D上封閉,則![]() .函數
.函數![]() 在
在![]() 上封閉,則
上封閉,則![]() ,
,
得到: ![]() .
.
![]() 在
在![]() 單調遞增.
單調遞增.
則![]()
![]() 在
在![]() 兩不等實根.
兩不等實根.
![]() ,
,
故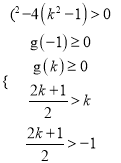 ,解得
,解得![]() .
.
另解: ![]() 在
在![]() 兩不等實根.令
兩不等實根.令![]()
![]() 在
在![]() 有兩個不等根,畫圖,由數形結合可知,
有兩個不等根,畫圖,由數形結合可知, ![]()
解得![]() .
.
(3)如果![]() ,則
,則![]() ,與題干
,與題干![]() 矛盾.
矛盾.
因此![]() ,取
,取![]() ,則
,則![]() .
.
接下來證明![]() ,因為
,因為![]() 是單射,因此取一個
是單射,因此取一個![]() ,
,
則![]() 是唯一的使得
是唯一的使得![]() 的根,換句話說
的根,換句話說![]()
考慮到![]() ,即
,即![]() ,
,
因為![]() 是單射,則
是單射,則![]()
這樣就有了![]() .
.
接著令![]() ,并重復上述論證證明
,并重復上述論證證明![]() ..
..


科目:高中數學 來源: 題型:
【題目】隨著我國經濟的快速發展,民用汽車的保有量也迅速增長.機動車保有量的發展影響到環境質量、交通安全、道路建設等諸多方面.在我國,尤其是大中型城市,機動車已成為城市空氣污染的重要來源.因此,合理預測機動車保有量是未來進行機動車污染防治規劃、道路發展規劃等的重要前提.從2012年到2016年,根據“云南省某市國民經濟和社會發展統計公報”中公布的數據,該市機動車保有量數據如表所示.
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代碼 | 1 | 2 | 3 | 4 | 5 |
機動車保有量 | 169 | 181 | 196 | 215 | 230 |
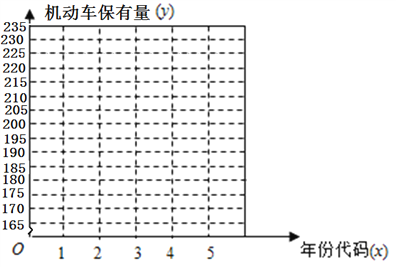
(1)在圖所給的坐標系中作出數據對應的散點圖;
(2)建立機動車保有量![]() 關于年份代碼
關于年份代碼![]() 的回歸方程;
的回歸方程;
(3)按照當前的變化趨勢,預測2017年該市機動車保有量.
附注:回歸直線方程![]() 中的斜率和截距的最小二乘估計公式分別為:
中的斜率和截距的最小二乘估計公式分別為:
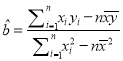 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() ,
, ![]() ,
, ![]() ,
, ![]() 滿足
滿足![]() ,且當
,且當![]() 時,
時, ![]() ,令
,令![]() .
.
(Ⅰ)寫出![]() 的所有可能的值.
的所有可能的值.
(Ⅱ)求![]() 的最大值.
的最大值.
(Ⅲ)是否存在數列![]() ,使得
,使得![]() ?若存在,求出數列
?若存在,求出數列![]() ;若不存在,說明理由.
;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知定圓![]() ,定直線
,定直線![]() ,過
,過![]() 的一條動直線
的一條動直線![]() 與直線相交于
與直線相交于![]() ,與圓
,與圓![]() 相交于
相交于![]() ,
,![]() 兩點,
兩點,![]() 是
是![]() 中點.
中點.
(Ⅰ)當![]() 與
與![]() 垂直時,求證:
垂直時,求證:![]() 過圓心
過圓心![]() ;
;
(Ⅱ)當![]() 時,求直線
時,求直線![]() 的方程;
的方程;
(Ⅲ)設![]() ,試問
,試問![]() 是否為定值,若為定值,請求出
是否為定值,若為定值,請求出![]() 的值;若不為定值,請說明理由.
的值;若不為定值,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱![]() 中,M,N分別為
中,M,N分別為![]() 的中點.
的中點.
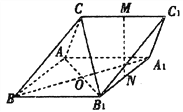
(1)證明:直線MN//平面CAB1;
(2)若四邊形ABB1A1是菱形,且![]() ,
, ![]() ,求平面
,求平面![]() 和平面
和平面![]() 所成的角(銳角)的余弦值.
所成的角(銳角)的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【選修4-4:坐標系與參數方程】
極坐標系的極點為直角坐標系![]() 的原點,極軸為
的原點,極軸為![]() 軸的正半軸,兩神坐標系中的長度單位相同.已知曲線
軸的正半軸,兩神坐標系中的長度單位相同.已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,
, ![]() .
.
(Ⅰ)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)在曲線![]() 上求一點,使它到直線
上求一點,使它到直線![]() :
: 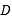 (
(![]() 為參數)的距離最短,寫出
為參數)的距離最短,寫出![]() 點的直角坐標.
點的直角坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com