
【題目】已知函數![]()
(Ⅰ)討論![]() 極值點的個數;
極值點的個數;
(Ⅱ)若![]() 是
是![]() 的一個極值點,且
的一個極值點,且![]() ,證明:
,證明:![]()
【答案】(Ⅰ)當![]() 時,
時,![]() 無極值點;當
無極值點;當![]() 時,
時,![]() 有1個極值點;
有1個極值點;
當![]() 或
或![]() ,
,![]() 有2個極值點.
有2個極值點.
(Ⅱ)見解析
【解析】
(Ⅰ)求導可得![]() ,再分
,再分![]() 與
與![]() 兩種情況進行討論即可.
兩種情況進行討論即可.
(Ⅱ)由(Ⅰ)以及![]() 可得
可得![]() ,再求得
,再求得![]() 關于
關于![]() 的解析式,再令
的解析式,再令![]() ,構造函數
,構造函數![]() ,再求導分析
,再求導分析![]() 的單調性與最值證明即可.
的單調性與最值證明即可.
解:(Ⅰ)由題得,![]() 的定義域為
的定義域為![]() ,
,![]()
ⅰ.若![]() ,則
,則![]() ,所以當
,所以當![]() 時,
時,![]() 單調遞減,
單調遞減,
當![]() 時,
時,![]() 單調遞增.
單調遞增.
所以,![]() 是
是![]() 唯一的極小值點,無極大值,故此時
唯一的極小值點,無極大值,故此時![]() 有且僅有1個極值點.
有且僅有1個極值點.
ⅱ. ![]() ,令
,令![]()
①當![]() 時,
時,![]() ,則當
,則當![]() 時,
時,![]() 單調遞增,
單調遞增,
當![]() ,
,![]() 單調遞減.
單調遞減.
所以,![]() 分別是
分別是![]() 極大值點和極小值點,故此時有兩個極值點.
極大值點和極小值點,故此時有兩個極值點.
②當![]() 時,
時,![]() 是
是![]() 的不變號零點,且
的不變號零點,且![]()
故此時![]() 在
在![]() 上單調遞增,無極值點.
上單調遞增,無極值點.
③當![]() 時,
時,![]() ,則
,則![]() 時,
時,![]() 單調遞增,
單調遞增,
當![]() 時,
時,![]() 單調遞減.
單調遞減.
所以,![]() 分別是
分別是![]() 極小值點和極大值點,此時
極小值點和極大值點,此時![]() 有2個極值點.
有2個極值點.
綜上,當![]() 時,
時,![]() 無極值點;當
無極值點;當![]() 時,
時,![]() 有1個極值點;
有1個極值點;
當![]() 或
或![]() ,
,![]() 有2個極值點.
有2個極值點.
(Ⅱ)證明:若![]() 是的一個極值點,
是的一個極值點,
由(Ⅰ)知,![]() 或
或![]() ,且
,且![]() ,
,
![]() ,
,
令![]() ,則
,則![]() ,所以
,所以![]()
故![]()
所以,當![]() 時,
時,![]() 單調遞增;當
單調遞增;當![]() 時,
時,![]() 單調遞減,
單調遞減,
所以![]() 是
是![]() 唯一極大值點也是最大值點,即
唯一極大值點也是最大值點,即 ![]() .
.
從而![]() ,即
,即![]() .(證畢)
.(證畢)


科目:高中數學 來源: 題型:
【題目】在如圖所示的幾何體中,四邊形ABCD為矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=2,點P在棱DF上.
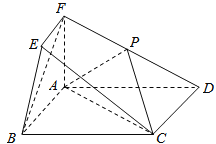
(1)若P是DF的中點,求異面直線BE與CP所成角的余弦值;
(2)若二面角D﹣AP﹣C的正弦值為![]() ,求PF的長度.
,求PF的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正項數列![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() ,且
,且![]() ,
,![]() (
(![]() 為常數).
為常數).
(1)求證:數列![]() 為等比數列;
為等比數列;
(2)若![]() ,且
,且![]() ,對任意
,對任意![]() ,
,![]() 都有
都有![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,是否存在正整數
,是否存在正整數![]() ,且
,且![]() ,使得
,使得![]() ,
,![]() ,
,![]() 三項成等比數列?
三項成等比數列?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“一帶一路”是“絲綢之路經濟帶”和“21世紀海上絲綢之路”的簡稱.某市為了了解人們對“一帶一路”的認知程度,對不同年齡和不同職業的人舉辦了一次“一帶一路”知識競賽,滿分100分(90分及以上為認知程度高).現從參賽者中抽取了![]() 人,按年齡分成5組,第一組:
人,按年齡分成5組,第一組: ![]() ,第二組:
,第二組: ![]() ,第三組:
,第三組: ![]() ,第四組:
,第四組: ![]() ,第五組:
,第五組: ![]() ,得到如圖所示的頻率分布直方圖,已知第一組有6人.
,得到如圖所示的頻率分布直方圖,已知第一組有6人.
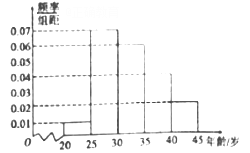
(1)求![]() ;
;
(2)求抽取的![]() 人的年齡的中位數(結果保留整數);
人的年齡的中位數(結果保留整數);
(3)從該市大學生、軍人、醫務人員、工人、個體戶 五種人中用分層抽樣的方法依次抽取6人,42人,36人,24人,12人,分別記為1~5組,從這5個按年齡分的組和5個按職業分的組中每組各選派1人參加知識競賽,分別代表相應組的成績,年齡組中1~5組的成績分別為93,96,97,94,90,職業組中1~5組的成績分別為93,98,94,95,90.
(Ⅰ)分別求5個年齡組和5個職業組成績的平均數和方差;
(Ⅱ)以上述數據為依據,評價5個年齡組和5個職業組對“一帶一路”的認知程度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年7月,中國良渚古城遺址獲準列入世界遺產名錄,標志著中華五千年文明史得到國際社會認可.良渚古城遺址是人類早期城市文明的范例,實證了中華五千年文明史.考古科學家在測定遺址年齡的過程中利用了“放射性物質因衰變而減少”這一規律.已知樣本中碳14的質量N隨時間T(單位:年)的衰變規律滿足![]() (
(![]() 表示碳14原有的質量),則經過5730年后,碳14的質量變為原來的______;經過測定,良渚古城遺址文物樣本中碳14的質量是原來的
表示碳14原有的質量),則經過5730年后,碳14的質量變為原來的______;經過測定,良渚古城遺址文物樣本中碳14的質量是原來的![]() 至
至![]() ,據此推測良渚古城存在的時期距今約在5730年到______年之間.(參考數據:
,據此推測良渚古城存在的時期距今約在5730年到______年之間.(參考數據:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】要得到![]() 的圖象
的圖象![]() ,只要將
,只要將![]() 圖象
圖象![]() 怎樣變化得到( )
怎樣變化得到( )
A.將![]() 的圖象
的圖象![]() 沿x軸方向向左平移
沿x軸方向向左平移![]() 個單位
個單位
B.將![]() 的圖象
的圖象![]() 沿x軸方向向右平移
沿x軸方向向右平移![]() 個單位
個單位
C.先作![]() 關于x軸對稱圖象
關于x軸對稱圖象![]() ,再將圖象
,再將圖象![]() 沿x軸方向向右平移
沿x軸方向向右平移![]() 個單位
個單位
D.先作![]() 關于x軸對稱圖象
關于x軸對稱圖象![]() ,再將圖象
,再將圖象![]() 沿x軸方向向左平移
沿x軸方向向左平移![]() 個單位
個單位
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】.(本小題滿分16分)
已知函數![]() ,并設
,并設![]() ,
,
(1)若![]() 圖像在
圖像在![]() 處的切線方程為
處的切線方程為![]() ,求
,求![]() 、
、![]() 的值;
的值;
(2)若函數![]() 是
是![]() 上單調遞減,則
上單調遞減,則
① 當![]() 時,試判斷
時,試判斷![]() 與
與![]() 的大小關系,并證明之;
的大小關系,并證明之;
② 對滿足題設條件的任意![]() 、
、![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍
的取值范圍
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com