Question

【題目】“一帶一路”是“絲綢之路經濟帶”和“21世紀海上絲綢之路”的簡稱．某市為了了解人們對“一帶一路”的認知程度，對不同年齡和不同職業的人舉辦了一次“一帶一路”知識競賽，滿分100分（90分及以上為認知程度高）.現從參賽者中抽取了人，按年齡分成5組，第一組： ，第二組： ，第三組： ，第四組： ，第五組： ，得到如圖所示的頻率分布直方圖，已知第一組有6人．

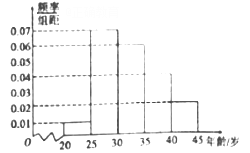
（1）求；

（2）求抽取的人的年齡的中位數（結果保留整數）；

（3）從該市大學生、軍人、醫務人員、工人、個體戶 五種人中用分層抽樣的方法依次抽取6人，42人，36人，24人，12人，分別記為1～5組，從這5個按年齡分的組和5個按職業分的組中每組各選派1人參加知識競賽，分別代表相應組的成績，年齡組中1～5組的成績分別為93，96，97，94，90，職業組中1～5組的成績分別為93，98，94，95，90．

（Ⅰ）分別求5個年齡組和5個職業組成績的平均數和方差；

（Ⅱ）以上述數據為依據，評價5個年齡組和5個職業組對“一帶一路”的認知程度．

Answer 1

【答案】（1）120；（2）32；（3）見解析

【解析】試題分析：（1）根據頻率分布直方圖求出第一組頻率，由此能求出；（2）設中位數為，則，由此能求出中位數；（3）①利用平均數公式和方差公式能分別求出個年齡組和個職業組成績的平均數和方差；②從平均數來看兩組的認知程度相同，從方差來看年齡組的認知程度更好.

試題解析：（1）根據頻率分布直方圖得第一組頻率為， ， ．

（2）設中位數為，則， ，中位數為32．

（3）（i）5個年齡組的平均數為，方差為．5個職業組的平均數為，方差為．

（ii）評價：從平均數來看兩組的認知程度相同，從方差來看年齡組的認知程度更好