【題目】已知橢圓
的離心率為
，其中左焦點
(-2,0).
（1） 求橢圓C的方程；
（2） 若直線y=x+m與橢圓C交于不同的兩點A，B，且線段AB的中點M在圓x2+y2=1上，求m的值.
【答案】19. 解①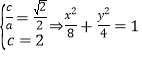
②設(shè)
由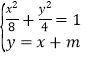
又
在
上
或
經(jīng)檢驗解題
或
【解析】
本試題主要是考查了橢圓方程的求解，以及直線與橢圓的位置關(guān)系的運用。
（1）由題意，得
得到a,b,c的值。得到橢圓的方程。
（2）設(shè)點A、B的坐標(biāo)分別為（x1,y1),(x2, y2)，線段AB的中點為M(x0,y0)，
由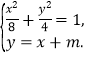
消y得，3x2+4mx+2m2-8=0結(jié)合韋達(dá)定理，和判別式得到參數(shù)m值。
解：（1） 由題意，得………………………………………………3分
解得
∴橢圓C的方程為
.…………………………………………6分
（2） 設(shè)點A、B的坐標(biāo)分別為（x1,y1),(x2, y2)，線段AB的中點為M(x0,y0)，
由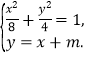消y得，3x2+4mx+2m2-8=0,……………………………………………8分
Δ=96-8m2＞0,∴-2
＜m＜2.
∴
.………………………………………12分
∵點M(x0,y0)在圓x2+y2=1上，
，
.………………………………………………… 14分
一諾書業(yè)暑假作業(yè)快樂假期云南美術(shù)出版社系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓C： 
=1（a＞b＞0）的短軸長為2，離心率e= 
．
（Ⅰ）求橢圓C的方程；
（Ⅱ）若直線l：y=kx+m與橢圓交于不同的兩點A，B，與圓x2+y2= 
相切于點M．
（i）證明：OA⊥OB（O為坐標(biāo)原點）；
（ii）設(shè)λ= 
，求實數(shù)λ的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖ABCD是平面四邊形，∠ADB=∠BCD=90°，AB=4，BD=2．
（Ⅰ）若BC=1，求AC的長；
（Ⅱ）若∠ACD=30°，求tan∠BDC的值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)函數(shù)
，曲線
在點
處的切線方程為
．
（1）求
，
的值；
（2）若
，求函數(shù)的單調(diào)區(qū)間；
（3）設(shè)函數(shù)
，且
在區(qū)間
內(nèi)為減函數(shù)，求實數(shù)
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某家具城進(jìn)行促銷活動，促銷方案是：顧客每消費滿1000元，便可以獲得獎券一張，每張獎券中獎的概率為
，若中獎，則家具城返還顧客現(xiàn)金1000元，某顧客購買一張價格為3400元的餐桌，得到3張獎券，設(shè)該顧客購買餐桌的實際支出為
（元）；
（1）求的所有可能取值；
（2）求的分布列和數(shù)學(xué)期望
；
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知a＞0，函數(shù)f（x）= 
+|lnx﹣a|，x∈[1，e2]．
（1）當(dāng)a=3時，求曲線y=f（x）在點（3，f（3））處的切線方程；
（2）若f（x）≤ 
恒成立，求實數(shù)a的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】函數(shù)y=ln（x2﹣4x+3）的單調(diào)減區(qū)間為（ ）
A. （2，+∞） B. （3，+∞） C. （﹣∞，2） D. （﹣∞，1）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
的長軸與短軸之和為6，橢圓上任一點到兩焦點
， 
的距離之和為4.
（1）求橢圓的標(biāo)準(zhǔn)方程；
（2）若直線
： 
與橢圓交于
， 
兩點， 
， 
在橢圓上，且
， 
兩點關(guān)于直線
對稱，問：是否存在實數(shù)
，使
，若存在，求出
的值；若不存在，請說明理由.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
(其中
是自然對數(shù)的底數(shù), 
=2.71828…).
(1)當(dāng)
時,過點
作曲線
的切線
，求的方程；
(2)當(dāng)
時,求證
;
(3)求證:對任意正整數(shù)
,都有
．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com